विषमबाहु त्रिभुज | Scalene Triangle in Hindi
विषमबाहु त्रिभुज ( Scalene Triangle) एक प्रकार का त्रिभुज होता है जिसकी तीन भुजाएं की लम्बाई असमान होती हैं। इसमें तीनों आंतरिक कोण भी अलग-अलग हैं।
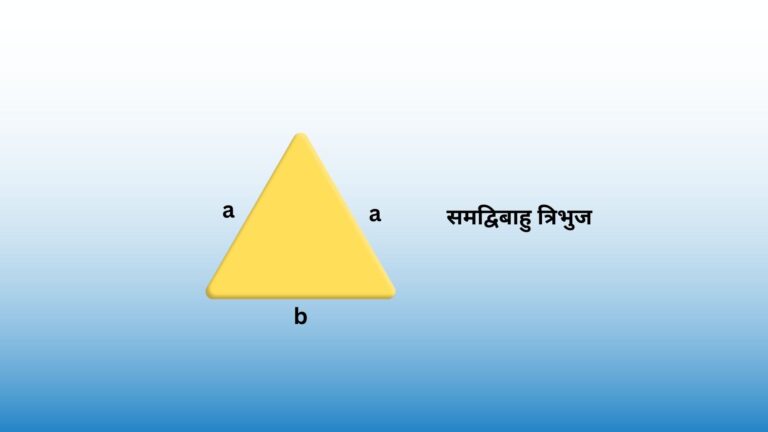
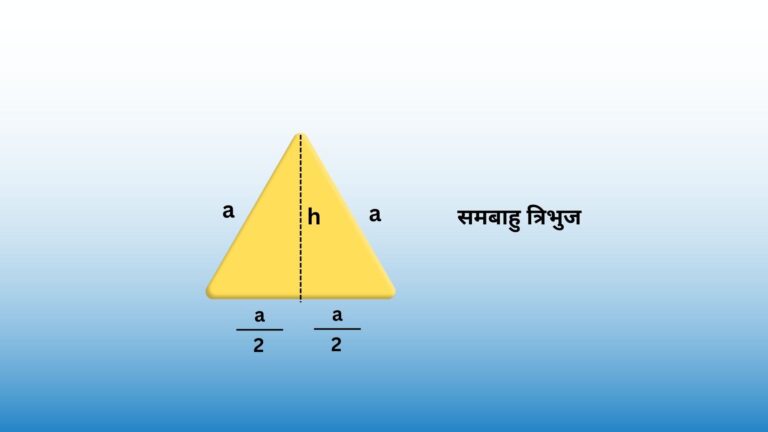
जैसे एक समद्विबाहु त्रिभुज की कम से कम दो भुजाएं समान लंबाई की होते हैं, या एक समबाहु त्रिभुज, जिसकी तीन भुजाएँ समान लंबाई की होते हैं।
Scalene triangle अन्य प्रकार के समबाहु (Equilateral) त्रिभुज, समद्विबाहु (Isosceles) त्रिभुज के बीच एक महत्वपूर्ण प्रकार का त्रिभुज है।
यदि परीक्षा की दृष्टि से भी देखें तो यह ज्यामिति के अंतर्गत त्रिभुज का एक महत्वपूर्ण अध्याय है।
इसलिए,
इस लेख में, मैंने इस विषय को बेहतर ढंग से समझने में आपकी मदद करने के लिए विषमबाहु त्रिभुज क्या है, गुण, कोण पर आधारित विषमबाहु त्रिभुज के प्रकार, महत्वपूर्ण सूत्र और विषमबाहु त्रिभुज के कुछ उदाहरण शामिल किए हैं।
यदि आप इस ब्लॉग के अंत तक प्रत्येक अनुभाग का अध्ययन करते हैं, तो मुझे यकीन है कि यदि विषमबाहु त्रिभुज के विषय पर प्रश्न पूछे जाएंगे तो आप आसानी से परीक्षा में अच्छा स्कोर कर पाएंगे।
चलो शुरू करते हैं
विषमबाहु त्रिभुज क्या है (Scalene triangle Definition)
एक त्रिभुज जिसमें कोई सर्वांगसम भुजाएँ या कोण नहीं होते हैं, विषमबाहु त्रिभुज कहलाते हैं। सरल शब्दों में, एक त्रिभुज जिसकी तीनो भुजाएँ की लंबाई समान नहीं होती हैं और तीनों आंतरिक कोण माप भी भिन्न होते हैं, विषमबाहु त्रिभुज कहलाते हैं।
प्रत्येक त्रिभुज अपनी भुजाओं और कोणों के आधार पर अद्वितीय होता है, तो आइए एक विषमबाहु त्रिभुज की अनूठी विशेषता को समझते हैं।
विषमबाहु त्रिभुज के गुण (Scalene triangle Properties)
विषमबाहु त्रिभुज के सबसे महत्वपूर्ण गुण इस प्रकार हैं:
- तीनों भुजाओं की लंबाई अलग-अलग है।
- विषमबाहु त्रिभुज के तीनों कोणों की माप अलग-अलग होती है।
- विषमबाहु त्रिभुज एकमात्र ऐसा त्रिभुज है जिसमें कोई सममित रेखा नहीं होती है।
- समरूपता का बिंदु नहीं है
- विषमबाहु त्रिभुज के आंतरिक कोणों का योग 180 डिग्री होता है।
- विषमबाहु त्रिभुज का आंतरिक कोण न्यून कोण , अधिक कोण या समकोण हो सकता है।
संबंधित लेख: त्रिभुज के गुण | Properties of Triangle in hindi
विषमबाहु त्रिभुज के प्रकार (Types)
विषमबाहु त्रिभुजों को उनके कोणों के आधार पर और वर्गीकृत किया जाता है।
- न्यून कोण विषमबाहु त्रिभुज
- समकोण विषमबाहु त्रिभुज
- अधिक कोण विषमबाहु त्रिभुज
उपरोक्त त्रिभुज क्या हैं? हम प्रत्येक को एक-एक कवर करेंगे।
न्यून कोण विषमबाहु त्रिभुज (Acute-angled Scalene triangle)
एक त्रिभुज एक न्यून कोण विषमबाहु त्रिभुज होता है, जब इसका एक कोण 90 डिग्री से कम मापता है और कोई भी भुजा लंबाई में बराबर नहीं होती है।
विषमबाहु त्रिभुज का उदाहरण 70°, 60°, 50° है
समकोण विषमबाहु त्रिभुज (Right-angled Scalene triangle)
एक विषमबाहु त्रिभुज जिसका एक कोण 90° के बराबर होता है, समकोण विषमबाहु त्रिभुज कहलाता है।
समकोण विषमबाहु त्रिभुज का उदाहरण 90°, 30°, 60° है
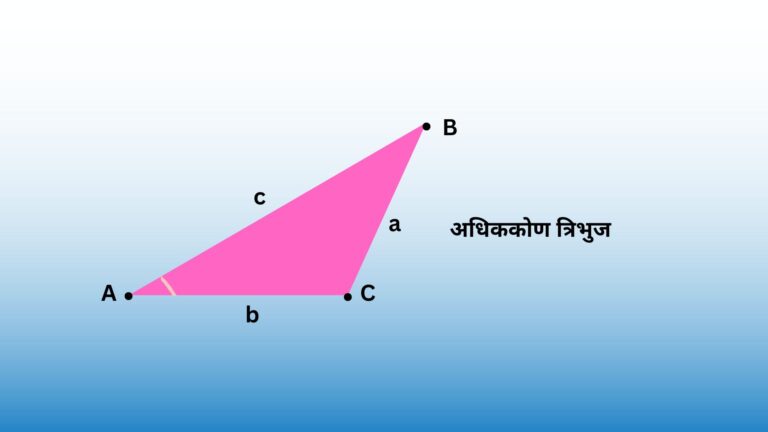
अधिक कोण विषमबाहु त्रिभुज (Obtuse-Angled Scalene triangle)
अधिक कोण विषमबाहु त्रिभुज एक ऐसा त्रिभुज होता है जिसका एक कोण 90 डिग्री से अधिक होता है और त्रिभुज की कोई भी भुजा लंबाई में बराबर नहीं होती है।
अधिक कोण विषमबाहु त्रिभुज का उदाहरण 110°, 40°, 30° है
विषमबाहु त्रिभुज के महत्वपूर्ण सूत्र (Important Formulas)
Scalene triangle की समस्याओं को हल करने के लिए उपयोग किए जाने वाले कई सूत्रों में से महत्वपूर्ण सूत्र निम्नलिखित हैं।
एक विषमबाहु त्रिभुज का क्षेत्रफल (Scalene triangle Area)
दिए गए आधार-सामग्री के आधार पर तीन सूत्रों में से किसी एक का उपयोग करके विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात किया जा सकता है।
- आधार और ऊंचाई का उपयोग करना
- Law of sines
- हीरोन का सूत्र
अगले भाग में, मैं विवरण में विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए उपरोक्त सूत्रों को शामिल करूँगा:
- आधार और ऊंचाई का उपयोग करना
विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए त्रिभुज का मूल सूत्र जब आधार और ऊँचाई दी गई हो = ½ *(b)*(h)
जहाँ b आधार है और h विषमबाहु त्रिभुज की ऊँचाई है।
- Law of sines
Law of sines का उपयोग लंबाई और कोण का उपयोग करके विषमबाहु त्रिभुज के क्षेत्रफल की गणना के लिए किया जा सकता है।
विषमबाहु त्रिभुज का क्षेत्रफल जब दो भुजाओं की लंबाई और उनके बीच के कोण की माप दी गई हो
विषमबाहु त्रिभुज का क्षेत्रफल = ½*(a)*(b)*(sinC)
जहाँ a, b भुजा की लंबाई हैं और C भुजाओं a और b के बीच का कोण है।
- हीरोन का सूत्र
विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए हीरोन के सूत्र का उपयोग तब किया जाएगा जब तीन भुजाओं की लंबाई दी गई हो।
त्रिभुज का क्षेत्रफल जब तीन भुजाओं की लंबाई दी गई हो = √ s(s-a)(s-b)(s-c)
a, b, और c त्रिभुज की भुजाओं की लंबाई हैं और s अर्ध-परिमाप है।
अर्ध-परिमाप (s) की गणना इस प्रकार की जा सकती है
अर्ध-परिमाप (s) = (a+b+c)/2
संबंधित लेख: त्रिभुज का क्षेत्रफल | Area of Triangle in Hindi
विषमबाहु त्रिभुज का परिमाप (Scalene triangle Perimeter)
विषमबाहु त्रिभुज का परिमाप ज्ञात करने के लिए बस तीनों भुजाओं की लंबाई को जोड़ दें।
विषमबाहु त्रिभुज का परिमाप a + b + c होता है
जहाँ a, b और c त्रिभुज की भुजाओं की लंबाई है।
संबंधित लेख: त्रिभुज का परिमाप | Perimeter of Triangle in Hindi
विषमबाहु त्रिभुज उदाहरण ( Examples)
उदाहरण 1: एक विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके आधार की लंबाई 6 सेमी और ऊंचाई की लंबाई 8 सेमी है।
हल: हम जानते हैं कि त्रिभुज का क्षेत्रफल निकालने का सूत्र = ½*(b)*(h)
दिया गया डाटा
b = 6 सेमी
h = 8 सेमी
विषमबाहु त्रिभुज के क्षेत्रफल का सूत्र = ½*(b)*(h)
= ½*(6 सेमी)*(8 सेमी)
= 1*(6 सेमी)*(4 सेमी)
= 24 सेमी⌃2
एक विषमबाहु त्रिभुज के 6 सेमी आधार और 8 सेमी ऊंचाई का क्षेत्रफल 24 सेमी⌃2 है
उदाहरण 2: एक विषमबाहु त्रिभुज का परिमाप ज्ञात कीजिए जिसके आधार की लंबाई 8 सेमी, एक भुजा की लंबाई 4 सेमी और दूसरी भुजा की लंबाई 12 सेमी है।
हल: विषमबाहु त्रिभुज का परिमाप a + b + c होता है
जहाँ a, b और c त्रिभुज की भुजा की लंबाई हैं
दिया गया डाटा:
ए = 8 सेमी
बी = 4 सेमी
सी = 12 सेमी
यदि हम मान को त्रिभुज की परिमाप में रखते हैं तो
= a + b + c
= 8 सेमी + 4 सेमी + 12 सेमी
= 24 सेमी
एक विषमबाहु त्रिभुज की भुजाओं की लंबाई 8 सेमी, 4 सेमी और 12 सेमी का परिमाप 24 सेमी है।
निष्कर्ष (conclusion)
विषमबाहु त्रिभुज, त्रिभुज के प्रकारों में से एक है। अन्य प्रकार के त्रिभुज, समबाहु त्रिभुज और समद्विबाहु त्रिभुज हैं।
इस लेख में मैंने विषमबाहु त्रिभुज से संबंधित सभी बातों को शामिल किया है। मुझे आशा है कि आप इसे अच्छी तरह समझ गए होंगे।
अगर मुझसे कोई विषय छूट गया हो तो मुझे संपर्क पेज के माध्यम से बताएं।