त्रिभुज का परिमाप | Perimeter of Triangle in Hindi
एक त्रिभुज एक बहुभुज है जिसमें तीन शीर्ष (vertices) और तीन सीधी भुजाएँ (sides) होती हैं। इस लेख में, हम त्रिभुज की परिमाप ज्ञात करने की विधियों के बारे में जानेंगे, त्रिभुज की परिमाप का निर्धारण कैसे करें, साथ ही हम अनेक विशेष त्रिभुज प्रकारों के परिमापों को भी देखेंगे।
आइए बेसिक (basic) के साथ शुरु करें:
त्रिभुज के परिमाप को परिभाषित करें
एक त्रिभुज का परिमाप उसकी सभी भुजाओं की कुल लंबाई है। सरल शब्दों में, किसी वस्तु या क्षेत्र के आकार या आयामों को मापने के लिए, उस पथ की लंबाई का उपयोग किया जाता है जो आकार को घेरता है। इस प्रकार, 2-D आकृति का परिमाप उसके चारों ओर के स्थान का माप है।
त्रिभुज के मामले में, आस-पास की जगह या इसके तीनों भुजाओं का जोड़ एक त्रिभुज की परिमाप है और हम त्रिभुज की परिमाप को रैखिक इकाई जैसे मीटर (m) या सेंटीमीटर (cm) में मापते हैं।
त्रिभुज का परिमाप ज्ञात करने की विधियाँ
किसी भी त्रिभुज का परिमाप ज्ञात करने की दो विधियाँ हैं
- जब तीन भुजाओं की लंबाई ज्ञात हो
- जब दो भुजाओं की लंबाई और उनके बीच का कोण दिया हो
पहले तरीके से शुरू करेंगे
एक त्रिभुज का परिमाप जब तीन भुजाओं की लंबाई दी गई हो
त्रिभुज की परिमाप निर्धारित करने के लिए निम्न सूत्र का उपयोग किया जा सकता है:
त्रिभुज का परिमाप = a + b + c
जहाँ “a,” “b,” और “c” त्रिभुज की भुजाओं की लंबाई को दर्शाता है।
उपरोक्त सूत्र का उपयोग करके परिमाप की गणना करने के लिए सरल अंग्रेजी में, इन सरल 2 चरणों का पालन करें:
- त्रिभुज की प्रत्येक भुजा की लंबाई मापें।
- तीनों भुजाओं की लंबाई को एक साथ जोड़ें।
उदाहरण के लिए, यदि त्रिभुज की भुजाओं की लंबाई 8 cm , 6 cm और 7 cm है, तो परिमाप की गणना इस प्रकार की जाएगी:
त्रिभुज का परिमाप = 8 cm + 6 cm + 7 cm = 21 cm
आइए दूसरी विधि देखें
जब दो भुजाओं की लंबाई और उनके बीच का कोण दिया गया हो
अब हम जानते हैं कि त्रिभुज का परिमाप त्रिभुज की तीन भुजाओं की लंबाई का योग होता है।
कोसाइन के नियम (Law of cosines) का उपयोग त्रिभुज में भुजाओं की लंबाई निर्धारित करने के लिए किया जा सकता है, जब आप अन्य दो भुजाओं की लंबाई और उनके बीच के कोण की माप जानते हों।
कोसाइन के नियम का सूत्र है (Law of cosines) : c⌃2 = a⌃2 + b⌃2 – 2ab cos(C)
जहाँ:
c कोण C के विपरीत भुजा की लंबाई है
a और b अन्य दो भुजाओं की लंबाई हैं
C, लंबाई c की भुजा के विपरीत कोण का माप है
Cos एक त्रिकोणमितीय अनुपात है जहाँ प्रत्येक कोण का एक भिन्न मान होता है जैसे Cos 60° = 0.5
विशेष प्रकार के त्रिभुज और उनकी परिमाप
मैं चार मुख्य प्रकार के त्रिभुजों को उनकी भुजाओं की लंबाई और कोणों के आधार पर कवर करूँगा।
- समबाहु त्रिभुज: सभी भुजाओं की लंबाई समान होती है
- समद्विबाहु त्रिभुज: दो भुजाओं की लंबाई समान होती है
- विषमबाहु त्रिभुज: सभी भुजाओं की लंबाई अलग-अलग होती है
- समकोण त्रिभुज: इसका एक आंतरिक कोण 90° का होता है
आइए पहले प्रकार के त्रिभुज से शुरू करें
एक समबाहु त्रिभुज का परिमाप (Perimeter of a Equilateral triangle)
एक त्रिभुज को समबाहु त्रिभुज कहा जाता है यदि इसकी तीनों भुजाओं की लंबाई समान हो।
और हम जानते हैं कि किसी भी त्रिभुज का परिमाप उसकी तीनों भुजाओं का योग होता है।
इसलिए,
एक समबाहु त्रिभुज की परिमाप की गणना करने के लिए, केवल एक भुजा की लंबाई को 3 से गुणा करें, क्योंकि सभी भुजाएँ समान हैं।
समबाहु त्रिभुज का परिमाप = 3*a
जहाँ a समबाहु त्रिभुज की एक भुजा की लंबाई है।
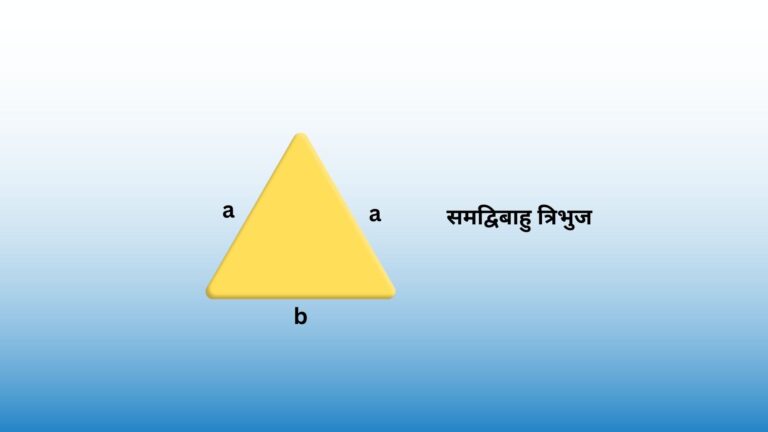
एक समद्विबाहु त्रिभुज का परिमाप (Perimeter of a Isosceles triangle)
एक त्रिभुज को समद्विबाहु त्रिभुज कहा जाता है यदि उसकी तीन में से दो भुजाओं की लंबाई समान हो।
और हम जानते हैं कि किसी भी त्रिभुज का परिमाप उसकी तीनों भुजाओं का योग होता है।
इसलिए,
एक समद्विबाहु त्रिभुज के लिए, पहले एक समद्विबाहु त्रिभुज की दो समान भुजाओं की लंबाई का योग करना चाहिए और फिर तीसरी भुजा की लंबाई को जोड़ना चाहिए।
समद्विबाहु त्रिभुज का परिमाप = 2*a+b
जहाँ a को दो समान भुजाओं में से एक की लंबाई चुनें और b शेष भुजा की लंबाई है।
नोट: यदि दो भुजाओं की लंबाई और उनके बीच बने कोण दिए गए हों, तो एक समद्विबाहु त्रिभुज का परिमाप ज्ञात करने के लिए शेष भुजा की लंबाई ज्ञात करने के लिए ऊपर दिया गया कोसाइन के नियम का उपयोग करें।
विषमबाहु त्रिभुज की परिमाप (Perimeter of Scalene triangle)
एक त्रिभुज को विषमबाहु त्रिभुज कहा जाता है यदि इसकी तीनों भुजाओं में से किसी की भी लंबाई समान नहीं है।
इसलिए,
विषमबाहु त्रिभुज का परिमाप ज्ञात करने के लिए, बस तीनों भुजाओं की लंबाई को एक साथ जोड़ दें।
अर्थात विषमबाहु त्रिभुज का परिमाप = a+b+c
जहाँ a, b और c त्रिभुज की लंबाई हैं।
अब आइए अंतिम त्रिभुज प्रकार के परिमाप को देखें।
समकोण त्रिभुज का परिमाप (Perimeter of Right angle triangle)
एक 90 डिग्री के कोण वाले त्रिभुज को समकोण त्रिभुज कहा जाता है।
एक समकोण त्रिभुज का परिमाप तीनों भुजाओं की लंबाई का योग होता है।
एक समकोण त्रिभुज का परिमाप = a+b+c
जहाँ a, b और c समकोण त्रिभुज की लंबाई हैं।
पाइथागोरस प्रमेय की बदौलत हम एक समकोण त्रिभुज की परिमाप के उपरोक्त सूत्र को सरल रूप में भी लिख सकते हैं।
उदाहरण के लिए:
मान लीजिए कि ⃤ ABC एक समकोण त्रिभुज है और ∠B समकोण अर्थात 90 डिग्री है। त्रिभुज ABC की तीन भुजाओं के नाम a, b और c हैं। जहाँ c कर्ण है और a, b पैर हैं।
पाइथागोरस प्रमेय का उपयोग करके c की लंबाई ज्ञात की जा सकती है अर्थात c = √a⌃2 + b⌃2
तो समकोण त्रिभुज का परिमाप = a+b+√a⌃2 + b⌃2
जहाँ a और b समकोण त्रिभुज के पाद (legs) हैं।
निष्कर्ष (Conclusion)
संक्षेप में, एक त्रिभुज की परिमाप उसकी सभी भुजाओं की कुल लंबाई है। इसकी गणना सूत्र का उपयोग करके की जा सकती है: परिमाप = a + b + c
जहाँ a, b और c त्रिभुज की लंबाई हैं।
मुझे आशा है कि आप सीख गए होंगे कि त्रिभुज का परिमाप कैसे निकाला जाता है।
यदि आपको यह मददगार लगता है, तो कृपया भविष्य में और अधिक अवधारणाएँ खोजने के लिए इस पृष्ठ को बुकमार्क कर लें।