त्रिभुज के महत्वपूर्ण भाग | Elements of Triangle in Hindi
एक तीन भुजाओं वाला बंद बहुभुज जो तीन सीधी रेखाओं और तीन आंतरिक कोणों से बना हो, त्रिभुज (Triangle) कहलाता है।
आरंभ करने से पहले, मैं यह कवर करना चाहता हूं कि यह विषय वास्तविक जीवन और परीक्षा के दृष्टिकोण से क्यों महत्वपूर्ण है।
त्रिभुज ज्यामिति का एक महत्वपूर्ण विषय है। त्रिभुज का वास्तविक जीवन में उपयोग जैसे ट्रस ब्रिज, सड़कें, ऊंची इमारतों आदि का निर्माण और यदि मैं परीक्षा के दृष्टिकोण से बात करता हूं तो त्रिभुज की समस्या को आसानी से हल करने के लिए त्रिभुज के तत्वों को जानना भी सहायक होता है।
तो,
इस लेख में क्या शामिल किया जाएगा?
इस लेख में, मैं सबसे पहले एक त्रिभुज के मूल तत्वों को कवर करूँगा, जिसमें इसके शीर्ष, भुजाएँ, कोण और ऊंचाई शामिल हैं। इसके प्रकारों के आधार पर त्रिभुज के और भी तत्व हैं, जैसे पाद, कर्ण, समकोण, न्यून कोण और अधिक कोण। इसके अतिरिक्त, मैं त्रिभुज के उन्नत तत्वों जैसे कि त्रिभुज की माध्यिका, लम्ब समद्विभाजक, और त्रिभुज के कोण समद्विभाजक को कवर करूँगा।
त्रिभुज के मूल भाग (Important Elements of triangle)
तो, आइए त्रिभुज के निम्नलिखित मूल तत्वों के साथ आरंभ करें।
शीर्ष (Vertices)
एक शीर्ष त्रिभुज के दो या दो से अधिक रेखा खंडों का प्रतिच्छेदन होता है। त्रिभुज में तीन शीर्ष होते हैं।
भुजा (Sides)
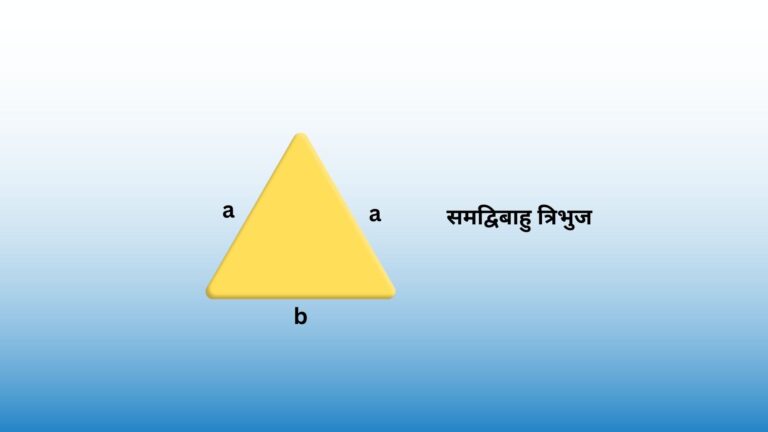
एक त्रिभुज की एक भुजा एक रेखाखंड है जो दो शीर्षों को जोड़ता है। त्रिभुज में तीन भुजाएं होती हैं।
भुजाओं की लंबाई के आधार पर त्रिभुज को तीन प्रकारों में विभाजित किया जाता है:
इसके अतिरिक्त कोणों और भुजाओं की लंबाई के आधार पर त्रिभुज के और भी प्रकार हैं। आप उन्हें यहाँ पढ़ सकते हैं।
कोण (Angles)
एक त्रिभुज का कोण एक उभयनिष्ठ शीर्ष साझा करने वाली दो भुजाओं की लंबाई के बीच आंतरिक स्थान का माप है। त्रिभुज में तीन कोण होते हैं।
एक त्रिभुज कोणों के आधार पर और विभाजित हो सकता है:
- न्यूनकोण त्रिभुज
- समकोण त्रिभुज
- अधिक कोण त्रिभुज
आंतरिक कोण (Interior angle)
एक त्रिभुज के आंतरिक कोण व कोण होते हैं जो त्रिभुज के अंदर तब बनते हैं जब दो भुजाएं शीर्ष पर मिलती हैं। त्रिभुज के आंतरिक कोणों का योग हमेशा 180 डिग्री होता है।
बाहरी कोण (Exterior Angle)
वे कोण जो त्रिभुज के बाहर होते हैं और त्रिभुज की किसी एक भुजा को बढ़ाकर बनाए जाते हैं, त्रिभुज के बाह्य कोण कहलाते हैं।
ऊंचाई (Height)
त्रिभुज के एक शीर्ष से विपरीत दिशाओं के मध्य बिंदु (आधार को भी संदर्भित करता है) तक खींची गई एक लंबवत रेखा खंड को त्रिभुज की ऊंचाई या शीर्षलंब कहा जाता है।
त्रिभुज की माध्यिका (Median of a Triangle)
एक त्रिभुज की माध्यिका एक शीर्ष से विपरीत दिशा के केंद्र तक रेखा खंड है।
आम तौर पर, किसी त्रिभुज की माध्यिका कुछ प्रकार के त्रिभुजों के लिए त्रिभुज की ऊंचाई के समान होती है। साथ ही, एक त्रिभुज की तीन माध्यिकाएँ त्रिभुज को समान क्षेत्रफल वाले छह छोटे त्रिभुजों में विभाजित करती हैं।
अक्सर परीक्षाओं में त्रिभुज की माध्यिका से प्रश्न आते हैं। इसलिए, मेरा सुझाव है कि आप इस पर और पढ़ें।
विभिन्न प्रकार के त्रिभुज के तत्व (Elements of other types of Triangle)
पाद (Legs)
एक समकोण त्रिभुज में, दो भुजाएँ जो समकोण (90°) बनाती हैं, पाद कहलाती हैं। जबकि एक समद्विबाहु त्रिभुज में, पाद दो सर्वांगसम भुजा या भुजाएं होती हैं जो लंबाई में समान होती हैं।
समकोण (Right angle)
एक समकोण त्रिभुज में, कोणों में से एक का माप 90 डिग्री होता है।
कर्ण (Hypotenuse)
एक समकोण त्रिभुज में कर्ण, समकोण के विपरीत भुजा होती है।
न्यूनकोण (Acute Angle)
त्रिभुज के वे कोण जिन्हें 90 डिग्री से कम मापा जाता है, न्यून कोण कहलाते हैं।
अधिक कोण (Obtuse Angle)
एक त्रिभुज के कोण जो 90 डिग्री से अधिक मापे जाते हैं, अधिक कोण कहलाते हैं।
त्रिभुज का लम्ब द्विभाजक (Perpendicular Bisector of a Triangle)
एक त्रिभुज का लम्ब समद्विभाजक एक रेखा खंड होता है जो त्रिभुज की एक भुजा पर लम्बवत होता है और समद्विभाजित करता है (दो बराबर हिस्सों में विभाजित करता है)।
त्रिभुज का कोण समद्विभाजक (Angle Bisector of a Triangle)
त्रिभुज का कोण समद्विभाजक एक रेखा खंड होता है जो त्रिभुज के कोण को समद्विभाजित करता है (आधा काटता है)।
एक त्रिभुज के तीन कोण समद्विभाजक त्रिभुज को अलग-अलग क्षेत्रफल वाले छोटे त्रिभुजों में विभाजित करते हैं।
निष्कर्ष (Conclusion)
आख़िरकार हम अंत में हैं और बस यह सब “त्रिभुज के तत्व” विषय में था। मुझे आशा है कि आप त्रिभुज के मूल तत्वों को समझ गए होंगे (शीर्ष, भुजा, कोण, आंतरिक कोण, बाहरी कोण, ऊँचाई)
एक त्रिभुज के अन्य तत्व (पाद, लम्बवत, माध्यिका आदि) भी महत्वपूर्ण हैं और मैं उन पर भी ध्यान केंद्रित करने की सलाह देता हूं।
किसी भी प्रकार की शंका या ठीक से समझ में न आने की स्थिति में। हमसे संपर्क करें Contact us page के माध्यम से मुझे बताएं, ताकि मैं सामग्री में सुधार कर सकूं।