त्रिभुज का क्षेत्रफल | Area of Triangle in Hindi

त्रिभुज का क्षेत्रफल (Area of triangle), त्रिभुज के आकार का एक माप है, और यह गणित ज्यामिति और कई अन्य क्षेत्रों में एक महत्वपूर्ण अवधारणा है।

इस ब्लॉग में, हम त्रिभुजों की मूल परिभाषा और त्रिभुज के क्षेत्रफल को कवर करेंगे, त्रिभुज के क्षेत्रफल की गणना के लिए मूल सूत्र की व्याख्या करेंगे, और त्रिभुज के क्षेत्रफल की गणना के लिए विभिन्न तरीकों पर चर्चा करेंगे, जिसमें हीरोन के सूत्र का उपयोग और त्रिकोणमितीय अनुपात इसमें शामिल है |

आएँ शुरू करें!

त्रिभुज मूल बातें (Triangle basics definition)

त्रिभुज (Triangle) ज्यामितीय आकृतियाँ हैं जो तीन रेखा खंडों से बनी होती हैं जिन्हें भुजाएँ (sides) कहा जाता है।

त्रिभुजों को उनकी भुजाओं की लंबाई (length) और उनके कोणों (angles) के आधार पर वर्गीकृत किया जा सकता है।

त्रिभुज के चार मुख्य प्रकार हैं

• समबाहु त्रिभुज (Equilateral triangle)
• समद्विबाहु त्रिभुज (Isosceles triangle)
• विषमबाहु त्रिभुज (Scalene triangle)
• समकोण त्रिभुज (Right angle triangle)

हम इस ब्लॉग में उपरोक्त त्रिभुज प्रकारों के लिए क्षेत्रफल देखेंगे।

यदि आप किसी विशिष्ट प्रकार के त्रिभुज का क्षेत्रफल ढूंढ रहे हैं तो बेझिझक अगले खंड को छोड़ दें और त्रिभुज का क्षेत्रफल ज्ञात करने के लिए किसी विशिष्ट खंड तक पहुंचने के लिए नीचे दिए गए लिंक पर क्लिक करें।

• समबाहु त्रिभुज का क्षेत्रफल (Area of Equilateral triangle)
• समद्विबाहु त्रिभुज का क्षेत्रफल (Area of Isosceles triangle)
• विषमबाहु त्रिभुज का क्षेत्रफल (Area of Scalene triangle)
• समकोण त्रिभुजों का क्षेत्रफल (Area of Right angle triangle)

त्रिभुज का क्षेत्रफल निकालने का मूल सूत्र सीखने के बाद विभिन्न प्रकार के त्रिभुजों का क्षेत्रफल देखेंगे। मैंने त्रिभुज का क्षेत्रफल ज्ञात करने के लिए एक से अधिक तरीकों को शामिल किया है।

लेकिन उसके पहले:

त्रिभुज के क्षेत्रफल की परिभाषा क्या है?

त्रिभुज का क्षेत्रफल उस स्थान की मात्रा है जो त्रिभुज द्वारा घिरा हुआ है और क्षेत्रफल की इकाई  m⌃2 (वर्ग मीटर) में हम मापते हैं|

त्रिभुज का क्षेत्रफल (Area of triangle)

अब आइए त्रिभुज का क्षेत्रफल ज्ञात करने की सटीक तरीका देखें।

त्रिभुज का क्षेत्रफल ज्ञात करने की तीन विधियाँ हैं।

• जब आधार और ऊंचाई दी गई हो।
• जब त्रिभुज की तीनों भुजाओं की लंबाई दी गई हो (हीरोन का सूत्र)।
• जब त्रिभुज की दो भुजाओं की लंबाई और उनके बीच का एक कोण ज्ञात हो।

आइए पहले से शुरू करें जब,

आधार और ऊंचाई दी गई हो:

त्रिभुज का क्षेत्रफल ज्ञात करने का मूल सूत्र:

त्रिभुज के क्षेत्रफल की गणना करने का मूल सूत्र = (आधार x ऊँचाई) / 2

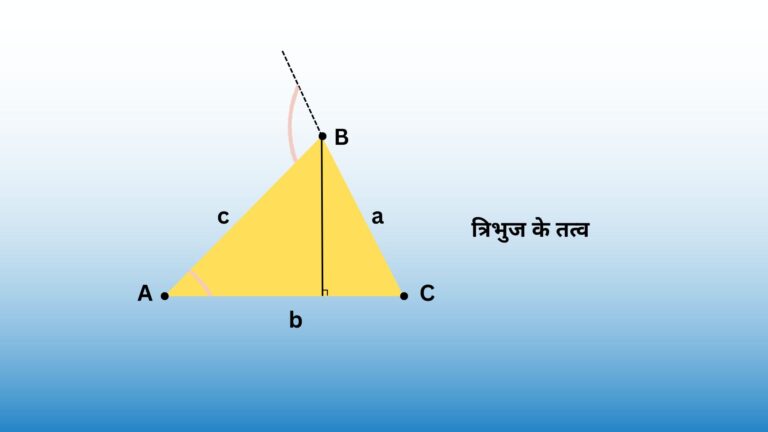
उपरोक्त सूत्र का उपयोग करने के लिए, आपको आधार की लंबाई और त्रिभुज की ऊंचाई की आवश्यकता है।

जहाँ आधार त्रिभुज की भुजाओं में से एक है और ऊँचाई आधार से विपरीत शीर्ष तक की लंबवत दूरी है।

जब त्रिभुज की तीनों भुजाओं की लंबाई दी गई हो (हीरोन का सूत्र):

जब त्रिभुज की तीनों भुजाओं की लंबाई दी गई हो तो हम त्रिभुज का क्षेत्रफल ज्ञात करने के लिए हीरोन के सूत्र का उपयोग करते हैं।

त्रिभुज का क्षेत्रफल जब भुजाओं की लंबाई दी गई हो = √ s(s-a)(s-b)(s-c)

a, b, और c त्रिभुज की भुजाओं की लंबाई हैं और s एक अर्धपरिमाप है। अर्धपरिमाप (s) ढूँढना आसान है।

अर्धपरिमाप (s) = (a+b+c)/2

यह आसान था, है ना?

जब त्रिभुज की दो भुजाओं की लंबाई और उनके बीच एक कोण दिया हो

त्रिभुज का क्षेत्रफल ज्ञात करने के लिए हम नीचे दिए गए सूत्र का उपयोग करेंगे जब त्रिभुज की दो भुजाओं (a और b, b और c, या c और a) की लंबाई और उनके बीच का कोण (A, B, C) ज्ञात हो .

दो भुजाओं वाले त्रिभुज का क्षेत्रफल a और b है और कोण C = 1/2 * a*b * sin C

दो भुजाओं वाले त्रिभुज का क्षेत्रफल b और c है और कोण A = 1/2 * b*c * sin A

दो भुजाओं वाले त्रिभुज का क्षेत्रफल c और a है और कोण B = 1/2 * c*a * sin B

Sin एक त्रिकोणमितीय अनुपात है जहाँ हर कोण का एक अलग मान होता है जैसे Sin 45° = 1/√2 है।

अब तक हमने त्रिभुज का क्षेत्रफल ज्ञात करने की तीन विधियों (methods) के बारे में बताया है।

आइए अब विभिन्न प्रकार के त्रिभुजों के क्षेत्रफल के बारे में जानें।

विभिन्न प्रकार के त्रिभुजों के क्षेत्रफल (Area of different types of triangle)

1. समबाहु त्रिभुज क्षेत्रफल (Equilateral triangle Area)

समबाहु त्रिभुज की तीन समान भुजाएँ और तीन समान कोण होते हैं।

समबाहु त्रिभुज का क्षेत्रफल है (√3/4)* (एक भुजा की लंबाई)

कोई भी भुजा की एक लंबाई रखें क्योंकि एक समबाहु त्रिभुज की सभी भुजाओं की लंबाई समान होती है।

पाइथागोरस प्रमेय का उपयोग करके ऊंचाई की लंबाई ज्ञात करके एक समबाहु त्रिभुज के उपरोक्त क्षेत्र को मूल सूत्र के माध्यम से प्राप्त किया जा सकता है!

2. समद्विबाहु त्रिभुज का क्षेत्रफल (Area of Isosceles triangle)

समद्विबाहु त्रिभुज की दो समान भुजाएँ और दो समान कोण होते हैं।

समद्विबाहु त्रिभुज का क्षेत्रफल (1/2)* (एक भुजा की लंबाई)⌃2 है

चूँकि समद्विबाहु त्रिभुज की दो भुजाएँ बराबर होती हैं, इसलिए हमने आधार की लंबाई और ऊँचाई को बराबर रखते हुए उपरोक्त सूत्र प्राप्त किया।

3. विषमबाहु त्रिभुज का क्षेत्रफल (Area of Scalene triangle)

विषमबाहु त्रिभुज की तीन असमान भुजाएँ और तीन असमान कोण होते हैं।

विषमबाहु त्रिभुज का क्षेत्रफल (आधार x ऊँचाई) / 2 है जब आधार और ऊँचाई दी गई हो।

4. समकोण त्रिभुजों का क्षेत्रफल (Area of Right angle triangle)

समकोण त्रिभुजों में एक समकोण होता है।

यदि त्रिभुज एक समकोण त्रिभुज है और पाद (कर्ण के विपरीत भुजाओं को पाद(legs) कहा जाता है) की लंबाई p और q है, तो त्रिभुज का क्षेत्रफल है = (p * q) / 2

यानी त्रिकोण के दो पैरों की लंबाई के गुणा को 2 से विभाजित।

निष्कर्ष (Conclusion):

त्रिभुज के क्षेत्रफल की गणना करते समय, आपको कुछ विशेष स्थितियों और कारकों को भी ध्यान में रखना होगा। उदाहरण के लिए, एक त्रिभुज का क्षेत्रफल शून्य होता है यदि इसकी भुजाओं की लंबाई शून्य या अनंत हो। इसके अतिरिक्त, एक त्रिभुज का क्षेत्रफल एक सम्मिश्र संख्या हो सकता है यदि इसकी भुजाओं की लम्बाई सम्मिश्र संख्याएँ हों।

मूल सूत्र या हीरोन के सूत्र और त्रिकोणमितीय अनुपात जैसी अतिरिक्त तकनीकों का उपयोग करके जानकारी के कई रूपों को देखते हुए त्रिभुज का क्षेत्रफल निर्धारित करना संभव है।

मुझे उम्मीद है कि मैंने जो कुछ खोजा है उसे मैंने कवर किया है। यदि नहीं, तो मुझे हमसे संपर्क करें पेज के माध्यम से बताएं।