क्षेत्रमिति
क्षेत्रमिति गणित की वह शाखा है जो लंबाई, आयतन, आकार, सतह क्षेत्र आदि जैसे मापदंडों पर 2डी और 3डी आंकड़ों के माप का अध्ययन कराती है। दूसरे शब्दों में, यह बीजगणितीय समीकरणों और गणितीय सूत्रों के आधार पर माप की प्रक्रिया भी है।
तो आइये आज के इस लेख में हम क्षेत्रमिति की अवधारणा और सूत्रों के बारे में अधिक विस्तार से जानें इसके अलावा और अधिक सपष्ट रूप से समझने के लिए कुछ उदाहरणों को हल करें। तो चलिए लेख शुरू करते हैं:-
क्षेत्रमिति क्या है?
क्षेत्रमिति को माप की एक क्रिया के रूप में बेहतरीन ढंग से समझाया जा सकता है। माप (measurement) की अवधारणा प्राथमिक और माध्यमिक विद्यालय के गणित में एक महत्वपूर्ण भूमिका निभाती है।
इसके अलावा, माप का हमारे रोजमर्रा के जीवन से सीधा संबंध है। वस्तुओं को मापना सीखते समय 3D आकृतियों और 2D आकृतियों दोनों के लिए मापना सीखते हैं।
वस्तुओं या मात्राओं को माप की मानक और गैरमानक दोनों इकाइयों का उपयोग करके मापा जा सकता है। उदाहरण के लिए, लंबाई मापने की एक गैर-मानक इकाई हैंडस्पैन होगी। ध्यान दें कि गैर-मानक इकाइयों का उपयोग करके वस्तुओं को मापते समय हमेशा विसंगति की गुंजाइश रहेगी। इसलिए माप की मानक इकाइयों की मदद से ही मापना सही होगा।
लंबाई, वजन और क्षमता जैसे मापदंडों को मापने के लिए अब हमारे पास किलोमीटर, मीटर, किलोग्राम, ग्राम, लीटर, मिलीलीटर आदि जैसी इकाइयाँ हैं।
3D आकृतियाँ
एक आकृति या ठोस जिसके तीन dimensions होते हैं उसे 3D आकृति कहा जाता है जिसमें फलक, किनारे और शीर्ष होते हैं। उनके पास एक सतह क्षेत्र है जिसमें उनके सभी चेहरों का क्षेत्र शामिल है। इन आकृतियों द्वारा घेरा गया स्थान उनका आयतन बताता है।
3डी आकृतियों के कुछ उदाहरण घन, घनाकार, शंकु, सिलेंडर हैं और कुछ वास्तविक दुनिया के उदाहरण एक किताब, एक जन्मदिन की टोपी और, एक कोक टिन हैं।
2D आकृतियाँ
ज्यामिति में, 2डी आकृतियों को समतल आकृतियों के रूप में परिभाषित किया जा सकता है जो पूरी तरह से सपाट होती हैं और उनके केवल दो dimensions होते हैं – लंबाई और चौड़ाई। इनमें कोई मोटाई नहीं होती और इन्हें केवल दो dimensions से ही मापा जा सकता है।
क्षेत्रमिति का उपयोग
वास्तविक जीवन परिदृश्यों में क्षेत्रमिति एक महत्वपूर्ण विषय है, इसके उपयोग के निम्न example है:-
- खरीद/बिक्री लेनदेन के लिए आवश्यक कृषि क्षेत्रों, फर्श क्षेत्रों का माप।
- दूध, तरल पदार्थ, ठोस खाद्य खाद्य पदार्थों की पैकेजिंग के लिए आवश्यक मात्रा का मापन।
- घरों, इमारतों आदि की पेंटिंग के आकलन के लिए आवश्यक सतह क्षेत्रों की माप।
- आयतन और ऊँचाई नदियों या झीलों में जल स्तर और मात्रा जानने में उपयोगी होते हैं।
- टेट्रा पैकिंग की तरह दूध आदि के लिए सही लागत पैकेजिंग पाउच।
क्षेत्रमिति से जुड़ी महत्वपूर्ण शर्तें
क्षेत्रमिति समतल आकृतियों और ठोस आकृतियों के माप से संबंधित है। आइए उपयोग किए गए कुछ महत्वपूर्ण शब्दों को जाने:-
| शब्द | परिभाषा |
| क्षेत्र | क्षेत्रफल एक द्वि-आयामी आकृति द्वारा घेरी गई जगह की मात्रा है। इसे वर्ग इकाइयों में व्यक्त किया जाता है। |
| परिमाप | परिधि आकृति के चारों ओर की कुल दूरी या किसी बंद आकृति की सीमा की लंबाई है। इसे वर्ग इकाइयों में व्यक्त किया जाता है। |
| आयतन | आयतन एक 3D आकृति द्वारा घेरी गई जगह की मात्रा है। इसे घन मीटर में व्यक्त किया जाता है। |
| सतह क्षेत्रफल | सतही क्षेत्रफल किसी 3D वस्तु की सतहों द्वारा घेरा गया कुल क्षेत्रफल है। उन्हें दो में वर्गीकृत किया गया है – घुमावदार या पार्श्व सतह क्षेत्र और कुल सतह क्षेत्र। |
क्षेत्रमिति सूत्र
क्षेत्रमिति सूत्रों में 3डी और 2डी दोनों आकार शामिल होते हैं। सबसे अधिक इस्तेमाल किया जाने वाला सूत्र इन आकृतियों का सतह क्षेत्र और आयतन है।
3डी आकार सूत्र
निम्न table विभिन्न 3D आकृतियाँ और उनके सूत्र दिखाती है –
| 3D आकार | सूत्र |
| गोला | व्यास = 2 × आर; (जहाँ ‘r’ त्रिज्या है)पृष्ठीय क्षेत्रफल = 4πr 2आयतन = (4/3)πr 3 |
| सिलेंडर | कुल सतही क्षेत्रफल = 2πr(h+r); (जहाँ ‘r’ त्रिज्या है और ‘h’ बेलन की ऊँचाई है)आयतन = πr 2 h |
| कोन | वक्र पृष्ठीय क्षेत्रफल = πrl; (जहाँ ‘l’ तिरछी ऊँचाई है और l = √(h 2 + r 2 ))कुल सतह क्षेत्रफल = πr(l + r)आयतन = (1/3)πr 2 h |
| घनक्षेत्र | पार्श्व सतही क्षेत्रफल = 4a 2 ; (जहाँ ‘a’ घन की भुजा की लंबाई है)कुल सतह क्षेत्रफल = 6a 2आयतन = a 3 |
| चश्मे | सतही क्षेत्रफल = [(2 × आधार क्षेत्रफल) + (परिधि × ऊँचाई)]आयतन = (आधार क्षेत्रफल × ऊँचाई) |
| घनाभ | पार्श्व सतही क्षेत्रफल = 2h(l + w); (जहां ‘h’ ऊंचाई है, ‘l’ लंबाई है और ‘w’ चौड़ाई है)कुल सतह क्षेत्र = 2 (lw + wh + lh)आयतन = (l × w × h) |
| पिरामिड | सतह क्षेत्र = आधार क्षेत्र + (1/2 × परिधि × तिरछी ऊंचाई)आयतन = [(1/3) × आधार क्षेत्र × ऊंचाई] |
2डी आकार सूत्र
निम्न तालिका उन सूत्रों को दिखाती है जिनका उपयोग कुछ सामान्य 2D आकृतियों के क्षेत्रफल और परिधि की गणना के लिए किया जाता है:
| 2D आकार | क्षेत्र सूत्र |
| घेरा | A = π × r 2 , जहां ‘r’ वृत्त की त्रिज्या है और ‘π’ एक स्थिरांक है जिसका मान 22/7 या 3.14 के रूप में लिया जाता है। परिधि (परिधि) = 2πr |
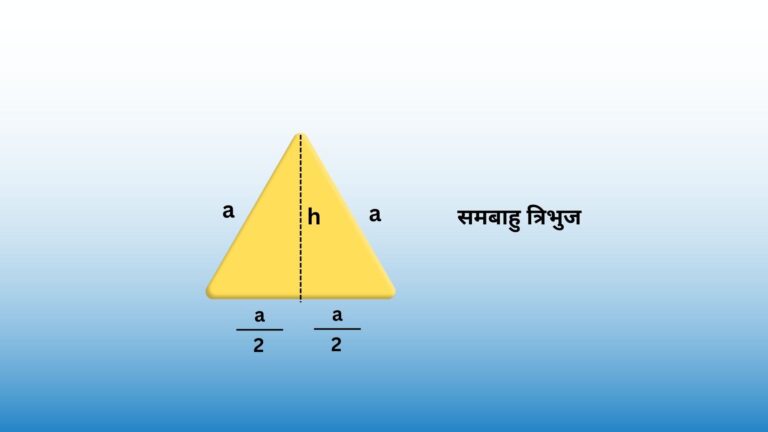
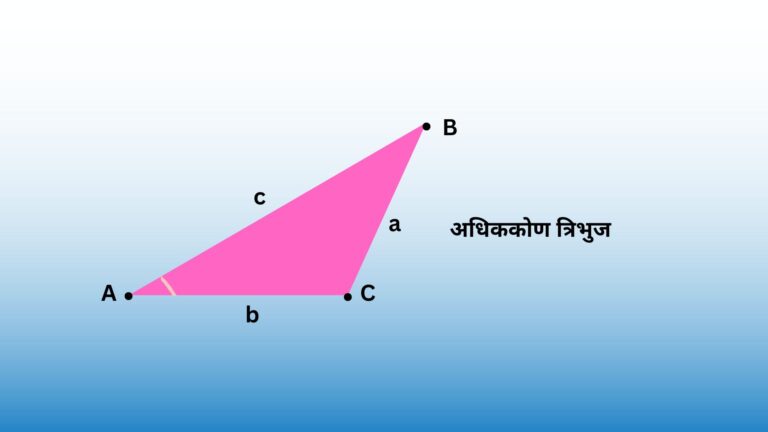
| त्रिकोण | क्षेत्रफल = ½ (आधार × ऊंचाई)परिमाप = तीनों भुजाओं का योग |
| वर्ग | क्षेत्रफल = भुजा 2 परिमाप = 4 × भुजा |
| आयत | क्षेत्रफल = लंबाई × चौड़ाईपरिमाप = 2 (लंबाई + चौड़ाई) |
क्षेत्रमिति के उदाहरण
उदाहरण 1: 5 सेमी भुजा वाले एक वर्ग का क्षेत्रफल ज्ञात करें।
समाधान :
वर्ग का क्षेत्रफल = भुजा × भुजा
यहाँ, भुजा = 5 सेमी
मानों को place करने पर, 5 × 5= 25.
वर्ग का क्षेत्रफल = 25 वर्ग cm.
उदाहरण 2: लंबाई 4 इकाई, चौड़ाई 5 इकाई और ऊंचाई 6 इकाई वाले घनाभ का सतह क्षेत्र ज्ञात करें।
समाधान:
दिया गया है,
घनाभ की लंबाई = 4 इकाई
घनाभ की चौड़ाई = 5 इकाई
घनाभ की ऊंचाई = 6 इकाई
घनाभ का पृष्ठीय क्षेत्रफल 2 × (lw + wh + lh) वर्ग इकाई है
= 2 × (lw + wh + lh)
= 2[(4 × 5) + (5 × 6) + (4 × 6)]
= 2(20 + 30 + 24)
= 2(74)
= 148 वर्ग इकाई.
उदाहरण 3: एक वृत्त का क्षेत्रफल ज्ञात करें जिसकी त्रिज्या 6 सेमी है।
समाधान: एक वृत्त 2डी आकृतियों की श्रेणी में आता है।
वृत्त का क्षेत्रफल = π × r 2
यहाँ ‘r’ वृत्त की त्रिज्या है और π एक स्थिरांक है, जिसका मान 22/7 या 3.14 है।
वृत्त का क्षेत्रफल = π × r 2
= 3.14 × 6 2
= 3.14 × 36
अत: वृत्त का क्षेत्रफल 113 होगा।
उदाहरण 4: एक त्रिभुज के आधार की length 15 मीटर तथा height 12 मीटर हैं। एक दूसरे त्रिभुज का क्षेत्रफल इस त्रिभुज के क्षेत्रफल का दुगुना हैं तथा इस त्रिभुज के आधार की लंबाई 20 मीटर हैं, इस त्रिभुज की ऊँचाई क्या होंगी?
A. 18 मीटर
B. 8 मीटर
C. 28 मीटर
D. 38 मीटर
हल:- पहले त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
= ½ (15 × 12)
= 90 वर्ग मीटर
दूसरे त्रिभुज का क्षेत्रफल = 2 × 90
क्षेत्रफल = 180 वर्ग मीटर
आधार = 20 मीटर
दूसरे त्रिभुज की ऊंचाई = (क्षेत्रफल × 2)/आधार
= (180 × 2)/20
Ans. 18 मीटर।
निष्कर्ष
दोस्तों, इस लेख में आपने क्षेत्रमिति के बारे में जानकारी प्राप्त की है। क्षेत्रमिति के अंतर्गत आने वाली 3D और 2D आकृतियां के बारे में आपने इस post के माध्यम से जाना है और साथ ही इनके सूत्रों के बारे में भी जाना है। हमने आपको उदाहरण के माध्यम से क्षेत्रमिति से जुड़े सवालों को स्पष्ट व सरल रूप से समझाने का प्रयास किया है। यदि अभी भी आपके मन में इस विषय से संबंधित कोई प्रश्न है तो आप हमें कमेंट कर के पूछ सकते हैं।इसके अलावा अगर किसी अन्य विषय पर जानकारी चाहते हैं तो उसके लिए भी कमेंट करके ज़रूर बताएं।