Cylinder, Cone, Cube: A Complete Geometry Guide with Pathyacram
“Your journey to a healthy lifestyle begins here.”
Understanding Cylinder, Cone, and Cube in Modern Geometry
Geometry forms the foundation of mathematical thinking, and three shapes that stand at the core of this subject are the cylinder, cone, and cube. These 3D shapes help students visualize space, volume, and structure, making complex topics easier to understand.
At Pathyacram, we focus on simplifying such concepts with clear explanations and real-world examples. Each of these shapes has its own properties, surface areas, and volumes, but when studied together, they provide a complete understanding of geometric reasoning.
These 3D shapes help students understand volume, surface area, and spatial structure through clear, visual concepts. In the middle of this learning journey, Pathyacram provides simple explanations, engaging visuals, and real-life examples that make each topic easier to grasp.
When learners explore the Cylinder, Cone, and Cube together, they develop a deeper and more connected understanding of geometric ideas and practical problem-solving.
Cylinder Structure, Formula, and Real-Life Meaning
Cone Applications and Mathematical Importance
1. Why Cylinders Matter
Understanding cylinders helps students calculate capacities and volumes used in engineering, packaging, and architecture. At Pathyacram, we teach how formulas like 2πrh and πr²h connect with daily life.
2.Why Cubes Are Important
Cubes play a crucial role in building strong geometric intuition because their equal faces and uniform edges make calculations easier to visualize. Students learn how cubes relate to real-world objects like building blocks, storage boxes, and architectural designs, helping them connect theory with practical observation.

Why Circles Matter in Geometry
At Pathyacram, we relate circles to real-life objects like wheels, rings, clocks, and circular tracks to make learning more meaningful. This approach helps students see how circular geometry.
Radius – the distance from the center to any point on the circle
Diameter – twice the radius, connecting two points across the center
Circumference – the total boundary length of the circle
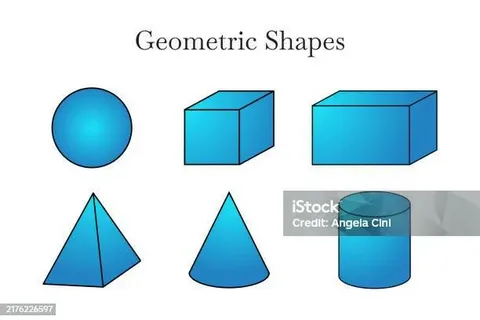



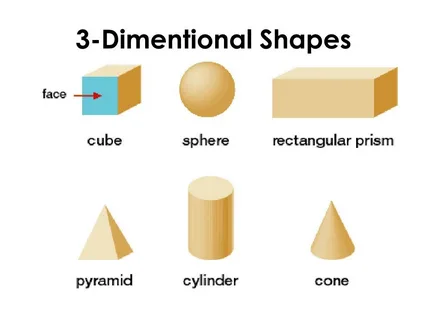
Cube – Perfect Symmetry and Mathematical Balance
Understanding Cones with Pathyacram
Cones are essential in concepts like frustums, slant height, and curved area. Students learn how cones help in calculating structures like towers, lampshades, and funnels with mathematical accuracy.The unique tapering shape of a cone makes it an important figure in engineering, design, and architectural modeling. When learners explore how the slant height relates to the curved surface area, they begin to understand how real-world objects are measured and constructed.
Importance of Trapezoids in Geometry
Students often encounter trapezoids in area calculation, architectural designs, and land measurement. Pathyacram ensures students fully understand how trapezoids contribute to the study of polygons.This shape is also widely used when calculating sloped surfaces, designing ramps, and analyzing irregular plots of land. By exploring different types of trapezoids like isosceles, right, and scalene students build stronger geometric judgment and analytical skills.
Geometry & Probability A Powerful Learning Combination
Geometry & Probability together create one of the most powerful and practical combinations in modern mathematics. While geometry focuses on shapes, measurements, distances, and spatial reasoning, probability deals with predicting outcomes and understanding uncertainty.When these two branches work together, students gain the ability to analyze real-world situations with both visual logic and statistical thinking. For example, probability models often use geometric diagrams, grids, regions, and shapes to calculate chances, areas of selection, and outcomes.
This connection helps learners visualize probability problems instead of treating them as abstract formulas. At Pathyacram, this blended approach is used to develop stronger reasoning skills, enabling students to interpret data, visualize scenarios, and make accurate predictions using geometric tools. Whether it’s determining the likelihood of landing in a shaded region, analyzing random points on shapes, or solving advanced coordinate geometry problems, the integration of Geometry And Probability strengthens decision-making and problem-solving abilities across academics, engineering, gaming strategies, and real-life planning.
Frequently Answer & question
1. Why are cylinder, cone, and cube important in geometry?
Ans These shapes help students understand spatial structure, surface area, and volume.They form the foundation for studying real-world objects and architectural designs.Learning them builds visual reasoning and strengthens problem-solving skills.
2. How does Pathyacram help students learn geometry?
Ans. Pathyacram explains concepts using simple language and visual examples.It connects shapes like circles, cubes, and trapezoids with real-life applications.This approach makes learning easier, faster, and more meaningful for students.
3.What is the role of probability in geometry?
Ans. Probability uses geometric diagrams and regions to calculate outcomes.Understanding shapes helps students visualize chance and uncertainty in problems.Together, geometry and probability improve logical thinking and accuracy.
4. What real-life objects are shaped like a cylinder, cone, or cube
Ans Cylinders appear in cans, bottles, and pipes.Cones are seen in traffic cones, ice cream cones, and funnels.
Cubes resemble gift boxes, dice, and building blocks.
5. Why is learning polygons important in geometry?
Ans Polygons form the base of many complex 2D and 3D shapes.They help students understand sides, angles, and shape construction.Learning polygons builds strong foundation skills for advanced geometry.
