वर्गमूल 

वर्गमूल एक ऐसी अवधारणा है, जो गणित में अक्सर इस्तेमाल की जाती है। यह एक ऐसी संख्या होती है जब इसे स्वयं की संख्या से गुणा किया जाता है तो जो प्राप्त गुणनफल होता है, वह उसका वर्ग होता है। और वही मूल संख्या उसका वर्गमूल बन जाती है। लेकिन अक्सर छात्रों को वर्गमूल की परिभाषा या सूत्र समझने में उलझन होती है।

इसलिए आज के इस लेख में हम वर्गमूल के बारे में सभी आवश्यक जानकारियां प्राप्त करेंगे, जिसमें वर्गमूल की परिभाषा, वर्गमूल के सूत्र, वर्गमूल ज्ञात करने की विधियां, इत्यादि सभी जानकारियाँ शामिल होंगी। 

वर्गमूल की परिभाषा

किसी संख्या का वर्गमूल वह संख्या होती है, जिसे अपने आप में गुणा करने पर मूल संख्या प्राप्त हो। यह एक संख्या को खोजने का तरीका है, जो स्वयं से गुणा करने पर मूल संख्या प्रदान करता है।

उदाहरण के लिए, 

4 का वर्गमूल दो होता है, क्योंकि अगर हम 2 संख्या को 2 से ही गुण करें तो हमें कर प्राप्त होगा।

√4 = 2

2 x 2 = 4

वर्गमूल का चिन्ह

वर्गमूल के चिन्ह को “√” दर्शाया जाता है। vargmul meaning in english स्क्वायर रूट ( Square Root) होता है। इस चिन्ह के नीचे जो संख्या लिखी होती है उसे “अध मूल राशि” कहते हैं। 

उदाहरण के लिए 6 का वर्गमूल लिखने के दो तरीके हैं –

√6 या 6 का वर्गमूल

यह दोनों ही एक ही चीज को दर्शाते हैं। बस एक 6 के साथ हमने वर्गमूल का चिन्ह लगाया है।

वर्गमूल सूत्र

वर्गमूल की परिभाषा एवं चिन्ह जानने के बाद लिए हम यह भी जान लेते हैं कि वर्गमूल निकालने के लिए किस सूत्र का उपयोग किया जाता है। 

वर्गमूल निकालने के लिए हम दो सूत्रों का उपयोग कर सकते हैं।

पूर्ण वर्ग संख्याओं का वर्गमूल निकालने के लिए, 

√a² = a

उदाहरण 

√9² = 9

अपूर्ण वर्ग संख्याओं का वर्गमूल निकालने के लिए

√a = b

जहाँ b वह संख्या है जो a के सबसे निकटतम पूर्ण वर्ग संख्या से कम है।

उदाहरण:

√10 = 3.16 (3.16² = 9.9856, जो 10 के सबसे निकटतम पूर्ण वर्ग संख्या से कम है)

वर्गमूल के गुण

वर्गमूल के गुण के माध्यम से आप वर्गमूल की परिभाषा एवं इसे ज्यादा बेहतर तरीके से समझ पाएंगे।

• अगर कोई संख्या पूरी तरह से अपने आप में गुणा होकर बनती है, तो उसका एकदम सही वर्गमूल होता है
• अगर किसी संख्या के अंत में दो या उससे ज्यादा जीरो (0) हों, तो उसका वर्गमूल हो सकता है।
• दो वर्गमूलों को आपस में गुणा किया जा सकता है, और नतीजा भी एक वर्गमूल होगा।
• यदि आप किसी एक ही संख्या का दो बार वर्गमूल निकालते हैं और उन्हें गुणा करते हैं, तो जवाब एक साधारण संख्या (गैर-वर्गमूल) होगा।
• यदि आप किसी एक ही संख्या का दो बार वर्गमूल निकालते हैं और उन्हें गुणा करते हैं, तो जवाब एक साधारण संख्या (गैर-वर्गमूल) होगा।
• अगर किसी संख्या का अंतिम अंक 2, 3, 7 या 8 है, तो उसका एकदम सही वर्गमूल नहीं हो सकता है. वहीं, अगर अंतिम अंक 1, 4, 5, 6 या 9 है, तो हो सकता है उसका एकदम सही वर्गमूल हो

संख्याओं का वर्गमूल ज्ञात करने की विधियां

अक्सर छात्रों का प्रश्न यह होता है कि वर्गमूल कैसे ज्ञात करें या वर्गमूल को कितने तरीके से निकाला जा सकता है। तो हम आपको बता दें कि वर्गमूल निकालने की चार अलग-अलग विधियां हैं। 

लेकिन यहां पर हमें पहले यह समझना होगा कि हमें किस तरह की संख्या का वर्गमूल निकालना है। जैसे अगर कोई पूरी संख्या होती है तो उसका वर्गमूल आसानी से निकाला जा सकता है।

उदाहरण के लिए 4, 9, 16, इनका वर्गमूल हम गुणनफल सारणी के मदद से निकाल सकते हैं। परंतु कुछ अधूरे वर्ग का वर्गमूल निकालने के लिए हमें अलग विधि का प्रयोग करना पड़ता है। उदाहरण के लिए 2, 3, 5 इत्यादि संख्याओं का वर्गमूल निकालना मुश्किल है।

वर्गमूल निकालने की चार विधियां -: 

1. अभाज्य गुणनखंड पद्धति द्वारा (Prime Factorisation Method)

जब आपके पास पूर्ण संख्या होती है तो यह तरीका वर्गमूल निकालने का सबसे आसान तरीका होता है। इससे हम संख्या को उसके अभाज्य गुणनखंडों में विभाजित करते हैं और फिर वर्गमुल निकलने हैं। 

उदाहरण के लिए, 

16 = 2x2x 2×2

√16 = 2×2 = 4

2. बार-बार घटाने की विधि (Repeated Subtraction Method)

इस विधि का उपयोग अब बहुत ही कम किया जाता है। लेकिन इसका उपयोग हम तब कर सकते हैं जब आपके पास पूर्ण संख्या हो। 

उदाहरण के लिए, 

25 – 1 = 24

24 – 3 = 21

21 – 5 = 16

16 – 7 = 9

9 – 9 = 0

यहाँ 25 को बार बार 5 बार घटाया गया है इसलिए 25 का वर्गमूल 5 होगा।

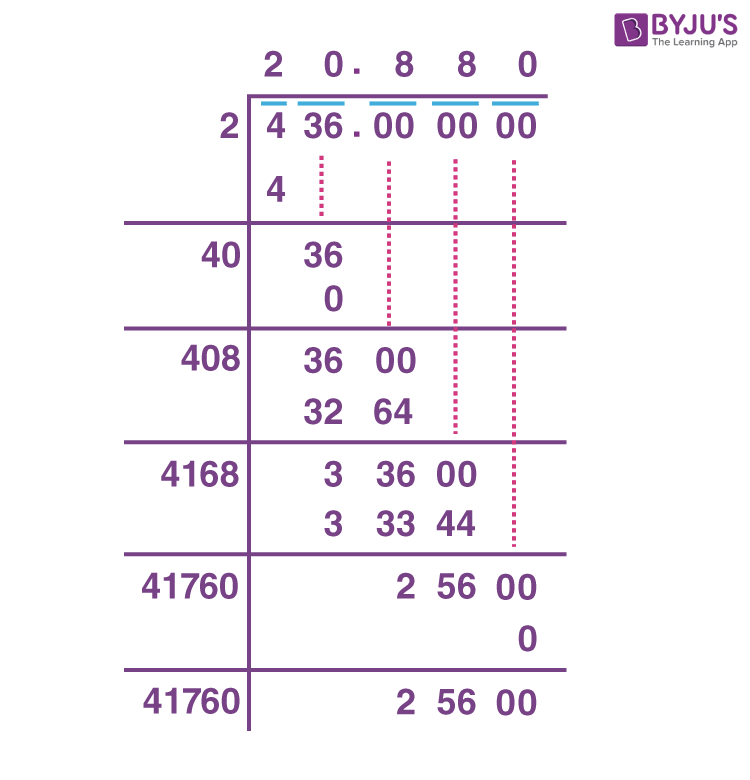
3. भाग विधि द्वारा (Division method)

भाग विधि वर्गमूल निकालने की एक ऐसी विधि है जो किसी भी तरीके की संख्या का वर्गमूल निकालने के लिए इस्तेमाल होता है। इस विधि में हम दी गई संख्या को अलग-अलग संख्याओं से भाग देते हैं।

आप चित्र में उदाहरण देख सकते है। 

4. आकलन विधि द्वारा (Estimation Method)

यह एक ऐसी विधि है, जिसके अंतर्गत हम अंदाजा लगाकर किसी संख्या का वर्गमूल निकलते हैं। इस विधि का उपयोग अधिकतर बड़ी संख्याओं का वर्गमूल निकालने के लिए किया जाता है।

उदाहरण के लिए, 

मान लीजिए आपको 5 का वर्गमूल निकालना है। तो आप जानते हैं कि 4 का वर्गमूल 2 है और 9 का वर्गमूल तीन है। तो अब आप अंदाजा लगा सकते हैं की 5 का वर्गमूल 2 और 3 के बीच ही होगा।

तब सवाल यह है कि 5 के करीब 2 है या 3 तो यहां आपको थोड़ा गणित लगाना होगा। जैसे सबसे पहले हम 2.2 और 2.8 का वर्ग निकालकर देखेंगे।

2.2 x 2.2 = 4.8

2.8 x 2.8 = 7.84

वर्ग निकालने पर आप देख सकते हैं कि 2.2 का वर्ग 5 के करीब है। तो इससे अंदाजा लगाया जा सकता है कि 5 का वर्गमूल 2.2 के आसपास होगा। 

पूर्ण वर्ग का वर्गमूल

नीचे हमने उन संख्याओं के बारे में जानकारी दी है, जो पूर्ण संख्याए हैं। इसके माध्यम से आप संख्याओं का वर्गमूल आसानी से निकाल सकते हैं। 

1² = 1	√1 = 1
2² = 4	√4 = 2
3² = 9	√9 = 3
4² = 16	√16 = 4
5² = 25	√25 = 5
6² = 36	√36 = 6
7² = 49	√49 = 7
8² = 64	√64 = 8
9² = 81	√81 = 9
10² = 100	√100 = 10

वर्गमूल सारणी

नीचे हमने 1 से 50 तक की वर्गमूल सारिणी प्रदान की है। जिससे आप याद कर सकते हैं, जिससे कि आपको बार-बार इन संख्याओं का वर्गमूल निकालने की जरूरत नहीं होगी।

वर्गमूल	मान	वर्गमूल	मान	वर्गमूल	मान
√1	1	√18	4.2426	√35	5.9161
√2	1.4142	√19	4.3589	√36	6
√3	1.7321	√20	4.4721	√37	6.0828
√4	2	√21	4.5826	√38	6.1644
√5	2.2361	√22	4.6904	√39	6.245
√6	2.4495	√23	4.7958	√40	6.3246
√7	2.6458	√24	4.899	√41	6.4031
√8	2.8284	√25	5	√42	6.4807
√9	3	√26	5.099	√43	6.5574
√10	3.1623	√27	5.1962	√44	6.6332
√11	3.3166	√28	5.2915	√45	6.7082
√12	3.4641	√29	5.3852	√46	6.7823
√13	3.6056	√30	5.4772	√47	6.8557
√14	3.7417	√31	5.5678	√48	6.9282
√15	3.873	√32	5.6569	√49	7
√16	4	√33	5.7446	√50	7.0711
√17	4.1231	√34	5.831

ऋणात्मक संख्या का वर्गमूल

ऋणात्मक संख्या का वर्गमूल वास्तविक संख्या नहीं होता है। ऐसा इसलिए है क्योंकि किसी भी पूर्णांक का वर्ग हमेशा धनात्मक संख्या ही होता है। मान लीजिए किसी ऋणात्मक संख्या को – y से दर्शाया गया है तो ऐसे में उसका वर्गमूल √(-y) होगा। 

इसे हम i√y लिख सकते है, जहां “i” -1 का वर्गमूल को दर्शाता है। इसे अवयव इकाई भी कहते हैं। इस तरह के वर्गमूलों को जटिल संख्याएं भी कहा जाता है। 

दशमलव का वर्गमूल

दशमलव का वर्गमूल ज्ञात करने के लिए आप नीचे दिए गए तरीके का इस्तेमाल कर सकते हैं।

उदाहरण:

√0.25 = √(25/100) = √25 / √100 = 5 / 10 = 0.5

वर्गमूलों के अनुप्रयोग

वर्गमूल गणित का एक महत्वपूर्ण हिस्सा है, और इसका इस्तेमाल हमारे दैनिक जीवन में भी कई चीजों को समझने और गणना करने में होता है. आइए देखें कि वर्गमूल का उपयोग किन-किन क्षेत्रों में किया जाता है:

• द्विघात समीकरण
• बीजगणित
• ज्यामिति
• गति, परिवर्तन, और मात्रा

निष्कर्ष

आज किस लेख में हमने वर्गमूल अवधारणा से संबंधित पूरी जानकारी प्राप्त की। साथ ही हमने वर्गमूल के सूत्र एवं ज्ञात करने की विधियों के बारे में भी जाना। यदि आप वर्गमूल विषय से संबंधित कोई अन्य जानकारी प्राप्त करना चाहते हो तो हमें कमेंट करके जरूर बताएं।