प्राकृतिक संख्याएँ: गणित का आधार

प्राकृतिक संख्याएँ गणित के बुनियादी निर्माण खंड हैं। वे अधिक जटिल गणितीय अवधारणाओं की नींव बनाते हैं, जिससे उन्हें गणितीय समस्याओं को समझने और हल करने के लिए आवश्यक बना दिया जाता है। 

इस लेख में, हम प्राकृतिक संख्याओं की परिभाषा, गुण, प्रकार, संचालन, संख्या प्रणाली और अनुप्रयोगों का पता लगाएंगे।

प्राकृतिक संख्याओं के उपयोग के दो वास्तविक जीवन के उदाहरण

लोगों की गिनती करना: विभिन्न परिदृश्यों में लोगों की संख्या की गणना करने के लिए आमतौर पर प्राकृतिक संख्या का उपयोग किया जाता है

खेल स्कोरिंग: विभिन्न खेलों में स्कोर करने में प्राकृतिक संख्याएँ महत्वपूर्ण भूमिका निभाती हैं

प्राकृतिक संख्या की परिभाषा (Natural numbers Definiton in Hindi)

प्राकृतिक संख्याएँ सकारात्मक पूर्णांक हैं जिनका उपयोग गिनती, आदेश देने और मापने के लिए किया जाता है। उन्हें “एन” प्रतीक द्वारा निरूपित किया जाता है और 1, 2, 3, 4, 5, और इसी तरह प्रदर्शित किया जाता है। प्राकृतिक संख्याओं का समुच्चय अनंत है, जिसका अर्थ है कि मौजूद प्राकृतिक संख्याओं की मात्रा की कोई ऊपरी 

सीमा नहीं है।

गणित में प्राकृतिक संख्या का महत्व

गणित में प्राकृतिक संख्याएँ महत्वपूर्ण हैं क्योंकि वे कई उच्च-स्तरीय गणितीय अवधारणाओं के लिए बिल्डिंग ब्लॉक्स के रूप में काम करती हैं। उनका उपयोग विभिन्न गणितीय क्रियाओं में किया जाता है, जैसे कि जोड़, घटाव, गुणा और भाग। इसके अलावा, समय, दूरी और मात्रा जैसी अवधारणाओं को व्यक्त करने के लिए प्राकृतिक संख्याओं का उपयोग किया जाता है।

प्राकृतिक संख्या का संक्षिप्त इतिहास

प्राकृतिक संख्याओं की अवधारणा प्राचीन काल से चली आ रही है, जहाँ उनका उपयोग मुख्य रूप से गिनती और मापने के लिए किया जाता था। प्राकृतिक संख्याओं को दर्शाने के लिए प्राचीन मिस्रवासियों, बेबीलोनियों और यूनानियों की अपनी-अपनी प्रणालियाँ थीं। हालाँकि, यह भारतीय गणितज्ञ आर्यभट्ट थे जिन्होंने शून्य के उपयोग सहित आधुनिक संख्या प्रणाली की शुरुआत की, जिसने गणित में प्राकृतिक संख्याओं के उपयोग के तरीके में क्रांति ला दी।

प्राकृतिक संख्या के गुण

प्राकृतिक संख्याओं में विभिन्न गुण होते हैं जो गणितीय समस्याओं को हल करने के लिए आवश्यक होते हैं। इन संपत्तियों में शामिल हैं:

संवृत गुण (क्लोजर प्रॉपर्टी)

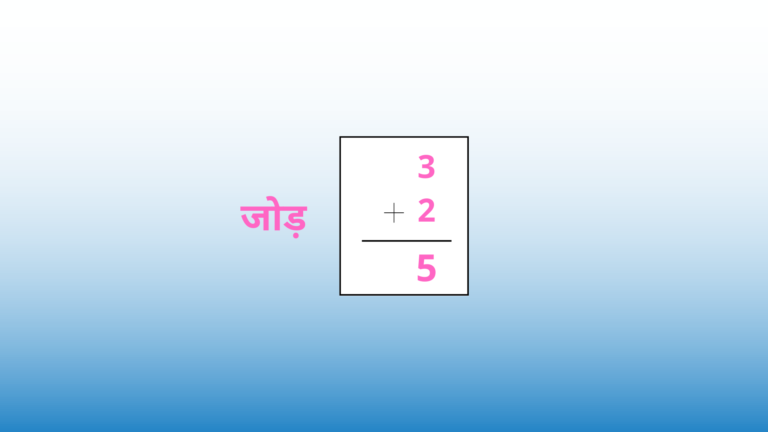
क्लोजर प्रॉपर्टी बताती है कि जब दो प्राकृतिक संख्याओं को जोड़ा जाता है, घटाया जाता है, गुणा किया जाता है या विभाजित किया जाता है, तो परिणाम हमेशा एक और प्राकृतिक संख्या होती है। उदाहरण के लिए, जब 2 और 3 को जोड़ा जाता है, तो परिणाम 5 आता है, जो कि एक प्राकृत संख्या भी है।

सहचर्य 

सहचर्य गुण बताती है कि जोड़ने या गुणा करने पर प्राकृतिक संख्याओं को कैसे समूहीकृत किया जाता है इसका क्रम परिणाम को प्रभावित नहीं करता है। उदाहरण के लिए, (2 + 3) + 4 = 2 + (3 + 4) और (2 x 3) x 4 = 2 x (3 x 4)।

क्रमविनिमेय गुण

क्रमविनिमेय गुण बताता है कि प्राकृतिक संख्याओं के क्रम को जोड़ने या गुणा करने पर परिणाम पर कोई प्रभाव नहीं पड़ता है। उदाहरण के लिए, 2 + 3 = 3 + 2 और 2 x 3 = 3 x 2।

वितरण की जाने वाली गुण 

वितरण गुण बताता है कि जब एक प्राकृतिक संख्या को दो प्राकृतिक संख्याओं के योग या अंतर से गुणा किया जाता है, तो परिणाम प्रत्येक प्राकृतिक संख्या को अलग-अलग गुणा करने और फिर परिणामों को जोड़ने या घटाने के समान होता है। उदाहरण के लिए, 2 x (3 + 4) = (2 x 3) + (2 x 4) और 2 x (4 – 3) = (2 x 4) – (2 x 3)।

पहचान गुण 

पहचान गुण बताती है कि जब एक प्राकृतिक संख्या को 1 से जोड़ा या गुणा किया जाता है, तो परिणाम हमेशा एक ही प्राकृतिक संख्या होती है। उदाहरण के लिए, 2 + 1 = 2 और 2 x 1 = 2।

व्युत्क्रम गुण 

व्युत्क्रम गुण  बताती है कि प्रत्येक प्राकृतिक संख्या के लिए, एक अद्वितीय योज्य या गुणक व्युत्क्रम मौजूद होता है, जिसे मूल संख्या के साथ क्रमशः जोड़ा या गुणा किया जाता है, जिसके परिणामस्वरूप पहचान तत्व होता है। उदाहरण के लिए, 2 का योज्य व्युत्क्रम -2 है, और 2 का गुणक प्रतिलोम 1/2 है।

प्राकृतिक संख्या के प्रकार

प्राकृतिक संख्याओं के प्रकारों पर चलते हुए, यह ध्यान रखना महत्वपूर्ण है कि प्राकृतिक संख्याओं के कई अलग-अलग वर्गीकरण हैं जिनका उपयोग उन्हें अलग-अलग तरीकों से वर्गीकृत करने के लिए किया जा सकता है। कुछ सबसे सामान्य प्रकार की प्राकृतिक संख्याएँ – अभाज्य संख्याएँ, मिश्रित संख्याएँ, विषम और सम संख्याएँ और पूर्ण संख्याएँ हैं।

अभाज्य प्राकृतिक संख्या

एक प्रमुख संख्या 1 से अधिक प्राकृतिक संख्या है जिसमें 1 और स्वयं के अलावा कोई सकारात्मक विभाजक नहीं है। दूसरे शब्दों में, एक अभाज्य संख्या एक संख्या है जिसे केवल 1 और स्वयं से ही समान रूप से विभाजित किया जा सकता है, और इसका कोई अन्य कारक नहीं है। 

अभाज्य संख्याओं के उदाहरणों में 2, 3, 5, 7, 11, और 13 शामिल हैं। अभाज्य संख्याएँ संख्या सिद्धांत, क्रिप्टोग्राफी और कंप्यूटर विज्ञान में बहुत महत्वपूर्ण हैं, और सदियों से बहुत अधिक अध्ययन का विषय रही हैं।

भाज्य प्राकृतिक संख्या

एक भाज्य संख्या 1 से अधिक प्राकृतिक संख्या है जो अभाज्य नहीं है। दूसरे शब्दों में, एक भाज्य संख्या एक संख्या है जिसे 1 और स्वयं के अलावा दो या दो से अधिक धनात्मक पूर्णांकों में विभाजित किया जा सकता है। भाज्य संख्याओं के उदाहरणों में 4, 6, 8, 9, 10 और 12 शामिल हैं। संख्या सिद्धांत में भाज्य संख्याओं का भी बहुत महत्व है और बड़े पैमाने पर अध्ययन किया गया है।

विषम और सम संख्याएँ

विषम और सम संख्याएँ प्राकृतिक संख्याओं को वर्गीकृत करने का एक और तरीका है। एक विषम संख्या एक प्राकृतिक संख्या है जो 2 से विभाज्य नहीं है, जिसका अर्थ है कि यह 2 से विभाजित होने पर 1 शेष छोड़ती है। विषम संख्याओं के उदाहरणों में 1, 3, 5, 7 और 9 शामिल हैं। सम संख्याएँ, दूसरी ओर, वे प्राकृतिक संख्याएँ हैं जो 2 से विभाज्य हैं, अर्थात 2 से भाग देने पर वे कोई शेष नहीं छोड़ती हैं। सम संख्याओं के उदाहरणों में 2, 4, 6, 8 और 10 शामिल हैं। विषम और सम संख्याओं के बीच का अंतर गणित के कई क्षेत्रों में उपयोगी है, ज्यामिति, बीजगणित और कलन सहित।

पूर्ण संख्या (परफेक्ट नंबर)

एक पूर्ण संख्या एक प्राकृतिक संख्या है जो इसके उचित विभाजकों के योग के बराबर होती है, या स्वयं संख्या के अलावा सकारात्मक विभाजक होती है। उदाहरण के लिए, पहली पूर्ण संख्या 6 है, क्योंकि इसके उचित विभाजक 1, 2 और 3 हैं, और 1 + 2 + 3 = 6 हैं। पूर्ण संख्याओं के अन्य उदाहरणों में 28, 496 और 8,128 शामिल हैं। पूर्ण संख्याएं अपेक्षाकृत दुर्लभ हैं, और पूरे इतिहास में बहुत अधिक आकर्षण और अध्ययन का विषय रही हैं।

यह भी पढ़ें: संख्या के प्रकार

प्राकृतिक संख्या पर संचालन

प्राकृतिक संख्याएँ अंकगणित के निर्माण खंड हैं। अंकगणित की सबसे मौलिक संक्रियाएं जोड़, घटाव, गुणा और भाग हैं। ये ऑपरेशन प्राकृतिक संख्याओं पर लागू होते हैं और इनका उपयोग जटिल गणना करने के लिए किया जा सकता है।

जोड़

योग दो या दो से अधिक संख्याओं को जोड़कर उनका योग प्राप्त करने की प्रक्रिया है। उदाहरण के लिए, 2 + 3 = 5, जहाँ 2 और 3 जोड़ हैं, और 5 योग है। योग में कई गुण होते हैं, जैसे क्रमविनिमेय गुण और साहचर्य गुण।

घटाव

घटाव दो संख्याओं के बीच अंतर खोजने की प्रक्रिया है। इसमें एक संख्या को दूसरी संख्या से दूर करना शामिल है। उदाहरण के लिए, 5 – 3 = 2, जहां 5 माइन्यूएंड है, 3 सबट्रेंड है, और 2 अंतर है।

गुणन

गुणन बार-बार जोड़ने की प्रक्रिया है। इसमें उनके उत्पाद को प्राप्त करने के लिए संख्याओं के समान समूहों को जोड़ना शामिल है। उदाहरण के लिए, 2 x 3 = 6, जहां 2 और 3 गुणनखंड हैं, और 6 गुणनफल है। गुणन में कई गुण होते हैं, जैसे क्रमविनिमेय गुण और वितरण गुण।

डिवीजन

विभाजन एक संख्या को समान भागों में विभाजित करने की प्रक्रिया है। इसमें यह पता लगाना शामिल है कि एक संख्या दूसरी संख्या में कितनी बार समाहित है। उदाहरण के लिए, 6 ÷ 2 = 3, जहां 6 भाज्य है, 2 भाजक है, और 3 भागफल है।

संख्या प्रणाली और प्राकृतिक संख्या

प्राकृतिक संख्याएँ संख्या प्रणाली का आधार हैं। हालांकि, वे एकमात्र प्रकार की संख्या नहीं हैं। कई अन्य प्रकार की संख्याएँ हैं, जैसे कि पूर्ण संख्याएँ, पूर्णांक, परिमेय संख्याएँ, अपरिमेय संख्याएँ, वास्तविक संख्याएँ और जटिल संख्याएँ।

पूर्ण संख्याएँ

पूर्ण संख्याएँ प्राकृतिक संख्याएँ और शून्य हैं। उनका उपयोग उन मात्राओं का प्रतिनिधित्व करने के लिए किया जाता है जिन्हें अंशों में विभाजित नहीं किया जा सकता है।

पूर्णांक

पूर्णांक पूर्ण संख्याएं और उनके ऋणात्मक होते हैं। उनका उपयोग उन मात्राओं का प्रतिनिधित्व करने के लिए किया जाता है जो सकारात्मक, नकारात्मक या शून्य हो सकती हैं।

परिमेय संख्याएँ

परिमेय संख्याएँ वे संख्याएँ होती हैं जिन्हें दो पूर्णांकों के अनुपात के रूप में व्यक्त किया जा सकता है। इनमें भिन्न और सांत दशमलव शामिल हैं।

अपरिमेय संख्या

अपरिमेय संख्याएँ वे संख्याएँ होती हैं जिन्हें दो पूर्णांकों के अनुपात के रूप में व्यक्त नहीं किया जा सकता है। इनमें गैर-समाप्ति वाले दशमलव शामिल हैं, जैसे पाई और वर्गमूल।

वास्तविक संख्या

वास्तविक संख्याएँ वे संख्याएँ होती हैं जिन्हें संख्या रेखा पर दर्शाया जा सकता है। इनमें सभी परिमेय और अपरिमेय संख्याएँ शामिल हैं।

जटिल संख्या

जटिल संख्याएँ वे संख्याएँ होती हैं जिन्हें a + bi के रूप में व्यक्त किया जा सकता है, जहाँ a और b वास्तविक संख्याएँ हैं और i काल्पनिक इकाई है। इनका उपयोग गणित की विभिन्न शाखाओं में किया जाता है, जैसे बीजगणित और कलन।

निष्कर्ष

अंत में, गणित और अन्य क्षेत्रों में प्राकृतिक संख्या एक आवश्यक और मौलिक अवधारणा है। उनका उपयोग मात्राओं का प्रतिनिधित्व करने, अंकगणितीय संचालन करने और समस्याओं को हल करने के लिए किया जाता है। प्राकृतिक संख्याओं में कई दिलचस्प गुण होते हैं, जैसे कि बंद करना, साहचर्य, क्रमविनिमेय, वितरण, पहचान और व्युत्क्रम गुण। कई प्रकार की प्राकृतिक संख्याएँ हैं, जैसे कि अभाज्य, भाज्य, विषम, सम और पूर्ण संख्याएँ, प्रत्येक अपने अद्वितीय गुणों और अनुप्रयोगों के साथ। प्राकृतिक संख्याओं का उपयोग विभिन्न संख्या प्रणालियों में भी किया जाता है, जैसे कि संपूर्ण, पूर्णांक, परिमेय, अपरिमेय, वास्तविक और जटिल संख्याएँ। अंत में, प्राकृतिक संख्याओं के गिनती और गणना, ज्यामिति और मापन, और कंप्यूटर विज्ञान में कई अनुप्रयोग हैं। प्राकृतिक संख्याओं और उनके अनुप्रयोगों पर आगे के शोध से विभिन्न क्षेत्रों में नई खोज और नवाचार हो सकते हैं।