Mastering Height and Distance: A Complete Guide with Pathyacram
“Your journey to a healthy lifestyle begins here.”
Key Concepts of Height and Distance
Understanding height and distance is a fundamental concept in mathematics, particularly in geometry and trigonometry. Students often encounter problems where they need to calculate the height of a building, tree, or tower, or determine the distance between two points using angles of elevation and depression. These problems are not just academic exercises; they have real-life applications in fields like construction, architecture, surveying, and navigation. At Pathyacram, we focus on simplifying these concepts and providing step-by-step guidance to help students master them effectively.
Mixture Problems: Combining Quantities
Mixture problems involve combining two or more substances in given ratios to achieve a desired concentration. These problems require careful calculations of quantities and percentages. By applying basic algebraic principles, students can determine the required amount of each component to achieve the desired mixture. Practicing these problems at Pathyacram strengthens analytical skills and improves accuracy in quantitative reasoning.
Permutation and Combination: Counting Techniques
Permutation and combination is an essential topic in probability and counting problems. It helps determine the number of ways objects can be arranged or selected, which is crucial in exams and real-life scenarios like arranging seats, forming teams, or scheduling events. Understanding the difference between permutations and combinations and applying formulas systematically is key to mastering this topic, and Pathyacram provides clear examples to simplify learning.
Time and Work; Time, Distance, and Speed
Time and work problems involve calculating how long it takes for one or more workers to complete a task. Similarly, time, distance, and speed problems help in understanding motion-related scenarios, such as traveling between two points or completing a journey. Both types of problems require logical reasoning, formula application, and practice. Pathyacram offers detailed strategies to solve these efficiently, saving time and minimizing errors.
Tables make it easy to organize and compare numerical values. Multiplication tables are a classic example that help students memorize facts quickly. Similarly, division tables show repeated subtraction and how numbers break down into smaller values.
Tap and Cistern; Races and Games
Tap and cistern problems are variations of time and work questions, where the focus is on filling or emptying containers. Races and games problems often involve relative speed and distance concepts, where understanding who finishes first or calculating differences in speed becomes essential. Regular practice of these problems with Pathyacram strengthens problem-solving skills and enhances exam readiness.
Races and games problems focus on comparing speeds, distances, and finishing times, often involving relative speed concepts. Practicing these types of questions regularly with Pathyacram helps students develop strong logical reasoning, improve calculation accuracy, and boost their overall problem-solving abilities for exams.
Practical Applications of Height and Distance
Height and distance problems are not just limited to textbooks—they have significant real-world applications. Engineers and architects use these concepts to design buildings, bridges, and towers accurately. Surveyors calculate distances across difficult terrains using angles of elevation and depression. Even pilots and sailors apply height and distance principles in navigation.
Cylinder Cone and Cube: 3D Applications
Time Management Techniques for Problem Solving
While learning formulas and methods is essential, time management is equally important for solving Height And Distance, time, and speed problems. Practicing regularly helps students identify shortcuts, avoid calculation errors, and improve speed during exams. Pathyacram provides not only detailed explanations but also timed exercises that train students to solve problems quickly without compromising accuracy.
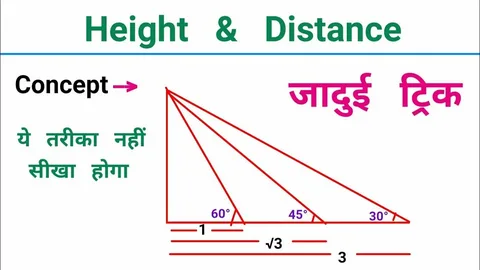
Common Mistakes to Avoid
Many students make errors while solving height and distance or related problems due to misreading angles, confusing formulas, or neglecting units of measurement. It is essential to carefully analyze each problem, draw diagrams, and apply trigonometric ratios correctly. Pathyacram emphasizes a systematic approach, teaching students how to identify pitfalls, verify answers, and build confidence in problem-solving.
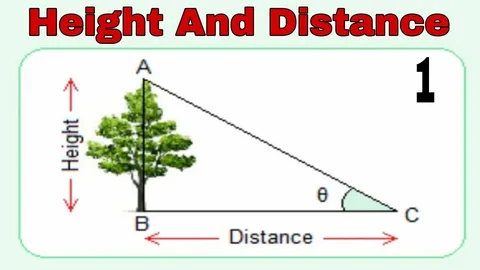



Understanding Height and Distance Concepts
Relative Speed in Races and Games
In races and games, relative speed plays a crucial role in determining the time difference or finishing order between competitors. Problems may involve calculating overtaking times, distance gaps, or simultaneous arrivals. Understanding these concepts helps students develop logical reasoning and improves performance in exams. Pathyacram teaches simple tricks and shortcuts to tackle these problems efficiently.
Tips for Visualizing 3D Geometry
Visualizing 3D shapes like Cylinders Cone Cube cones can be challenging for many students. Drawing 3D diagrams, using grid paper, or creating mental models of the shapes can significantly improve understanding. This visualization helps in solving problems related to heights, volumes, surface areas, and slant heights. Pathyacram emphasizes visualization techniques to strengthen spatial reasoning and improve problem-solving accuracy.
Motion Based Problems: Time, Distance, Speed, and Races
Problems related to motion, including time, distance, and speed or races and games, test a student’s ability to analyze moving objects and relative motion. By calculating speeds, distances, or finishing times, students can solve practical scenarios efficiently. Consistent practice with Pathyacram enables students to understand patterns, identify shortcuts, and apply formulas correctly under exam conditions.
These problems often require calculating travel times, distances covered, or comparing speeds between participants to determine outcomes. Regular practice with Pathyacram helps students develop analytical thinking, recognize patterns quickly, and apply formulas accurately, ensuring they can solve these problems efficiently during exams and real-life situations.
Practicing these problems regularly with Pathyacram allows students to identify patterns, apply formulas quickly, and solve problems accurately under exam conditions. Visualization techniques, such as drawing motion diagrams or marking distances and speeds on a line, further help in simplifying complex problems. Over time, consistent practice improves not only calculation speed but also logical reasoning, making students confident in tackling both standard and challenging motion-related questions.
Conclusion
Mastering height and distance is crucial for both academic success and real-life problem-solving. From basic trigonometry to advanced 3D shapes, mixtures, and motion-related problems, understanding these concepts strengthens analytical and reasoning skills. At Pathyacram, students receive clear explanations, step-by-step examples, and practical tips to solve problems confidently. Regular practice of these topics ensures not only exam readiness but also a strong foundation in mathematics that can be applied across diverse fields.
Frequently Asked Questions
Q1 How do I calculate the height of a building using angles?
Ans You can calculate the height using the tangent ratio in a right-angled triangle. Measure the distance from the building and the angle of elevation to the top, then apply height = distance × tan(angle). Practicing these calculations with examples improves accuracy.
2. Can height and distance concepts be applied in real life?
Ans Yes, these concepts are widely used in construction, navigation, and surveying. For example, engineers use angles and distances to measure heights of structures without physically climbing them. Learning these techniques with Pathyacram makes real-life applications easier to understand.
3. Are 3D shapes like cubes and cones important for height and distance problems?
Ans Absolutely. Many real-life problems involve volumes and surface areas of 3D objects. Understanding the dimensions, including heights, allows accurate calculation of space, material requirements, and structural design.
4.What is the role of angles of elevation and depression in height and distance problems?
Ans Angles of elevation and depression help measure the height or distance of objects without direct measurement. By using these angles with trigonometric ratios like tangent, sine, and cosine, students can calculate unknown heights or distances accurately. Pathyacram provides step-by-step examples to master these concepts efficiently.
5.How can I solve tap and cistern problems easily?
Ans Tap and cistern problems involve calculating the time taken to fill or empty a tank using rates of individual taps. To solve them, determine the net rate by combining filling and emptying rates, then divide the total capacity by this rate. Practicing these problems with Pathyacram strengthens speed and accuracy.
