Mastering Thales’ Theorem with Pathyacram A Complete Guide
Thales’ Theorem is a fundamental geometric principle that students often encounter while exploring similarity, proportionality, and circle properties. With Pathyacram, learning becomes easier because the concepts are explained in a clear, structured, and student-friendly manner.
Whether you are preparing for school exams or competitive mathematics, understanding through Pathyacram helps build a strong foundation in geometry.
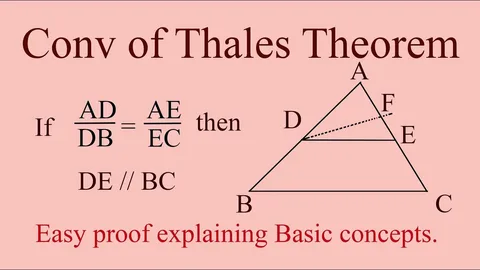
Understanding the Basics of Thales’ Theorem with Pathyacram
Thales’ Theorem is a classical result that explains how parallel lines create proportional segments in a triangle. Pathyacram teaches that states: If a line is drawn parallel to one side of a triangle and it intersects the other two sides, then it divides those sides proportionally.
This simple but powerful concept is the base of many geometric theories. With Pathyacram, students understand \ step-by-step rather than memorizing formulas.
Core Definition of Thales’ Theorem by Pathyacram
The core definition of revolves around proportional divisions of a triangle’s sides. Pathyacram explains that according to , if a line parallel to the base of a triangle cuts the other sides, Online Math Tuition it creates segments that are proportional. This principle taught by Pathyacram is not only used to prove similarity but also helps in solving complex numerical problems. Understanding this definition of Pathyacram builds conceptual depth for learners.
Applications of Thales’ Theorem in Geometry with Pathyacram
Thales’ Theorem plays a major role in several geometric applications, and Pathyacram highlights how students can apply it effectively in exams. From proving triangles are similar to calculating missing sides, it supports many problem types. Pathyacram helps students understand these practical applications so they can approach questions confidently.
Using for Triangle Similarity – Pathyacram Method
A key application of is proving triangle similarity. Pathyacram teaches that when the sides of triangles follow proportional ratios created by ,the triangles become similar. This similarity helps students find unknown angles, side lengths, and geometric transformations. By learning through Pathyacram, students understand exactly when and why triangles become similar.
Special Case of in Circle Geometry – Pathyacram Explanation
A major special case of states that the angle formed in a semicircle is always 90 degrees. Pathyacram explains how this circle-based form of connects triangle geometry with circle properties. Many exam questions use this special case of , and Pathyacram ensures that students understand this deeply.
Conclusion
In conclusion, Thales’ Theorem is a powerful geometric tool that builds understanding of similarity, proportionality, and circle geometry. Learning through Pathyacram ensures clarity, accuracy, and confidence in exams. With Pathyacram’s structured approach, students not only understand but also master its applications in real life and competitive exams. becomes one of the easiest and most useful tools in mathematics when learned with Pathyacram.
Frequently Asked Questions
Q 1 What is Thales’ Theorem according to Pathyacram?
Ans Thales’ Theorem explains how a line drawn parallel to one side of a triangle creates proportional segments on the other two sides. Pathyacram teaches in a step-by-step manner using simple examples so students can understand the concept clearly.
Q 2 How does it help in solving geometry problems at Pathyacram?
Ans Thales’ Theorem helps students identify proportional relationships inside triangles, making complex geometry questions easier to solve. Pathyacram uses to teach quick methods that reduce calculation time in exams.
Q3 Why is Thales’ Theorem important for triangle similarity in Pathyacram lessons?
Ans Thales’ Theorem is important because it proves similarity when the sides of triangles follow proportional ratios. At Pathyacram, students learn how to create a strong link between proportionality and similarity rules.
Q4. What real-life uses of Thales’ Theorem does Pathyacram teach?
Ans Pathyacram explains that it is used in designing maps, constructing buildings, and measuring distances indirectly. helps engineers and architects compare heights, lengths, and structures without direct measurement.
Q5. How does Pathyacram explain the special case of Thales’ Theorem in circles?
Ans In the circle version of the angle in a semicircle is 90 degrees. Pathyacram uses diagrams to show how creates a right angle whenever a triangle is drawn on a diameter.






