बहुभुज
गणित में बहुभुज एक ऐसी आकृति होती है, जो कई सीधी रेखाओं से मिलकर बनी होती है। यह एक द्वि-आयामी आकृति है। इसके कई सारी भुजाएं होती हैं। अक्सर छात्र बहुभूज जैसी आकृतियों को समझने में कंफ्यूज हो जाते हैं। इसलिए आज के इस लेख में हम बहुभुज की परिभाषा को विस्तार से जानेंगे।
साथ ही हम इस लेख में बहुभुज के प्रकार, बहुभुज का चित्र, बहुभुज की सूत्र, इत्यादि विषयों पर भी चर्चा करेंगे। तो लिए लेख को शुरू करें।
बहुभुज किसे कहते हैं?
बहुभुज एक समतल आकृति होती है, जिसे कई सीधी रेखाओं द्वारा बनाया जाता है। यह रेखाएं एक दूसरे से एक विशेष क्रम में इस प्रकार मिलते हैं कि वह एक बंद आकृति का निर्माण करते हैं और इसे ही बहुभुज कहा जाता है।
बहुभुज में कई सारी भुजाएं शामिल होती हैं, इसीलिए इसका नाम बहुभुज रखा गया है। बहुभुज में जहां दो भुजाएं एक साथ मिलती हैं और एक बिंदु का निर्माण करती हैं वह बिंदु शीर्ष कहलाता है या इसे कोना भी कह सकते हैं।
आसान शब्दों में समझे तो अनेक भुजाओं वाली आकृतियों को ही बहुभुज कहा जाता है।
बहुभुज की आकृति
बहुभुज की आकृति विभिन्न प्रकार की हो सकती है। बहुभुज में दो से लेकर कई सारी भुजाएं शामिल हो सकती है। बहुभुज के विभिन्न आकारों के उदाहरण त्रिभुज चतुर्भुज पंचभुज कष्टभुज अष्टभुजा इत्यादि हैं।
जैसे त्रिभुज में तीन भुजाएं हैं तो यह भी एक बहुभुज का ही एक उदाहरण होगा। बहुभुज के चित्र के माध्यम से आप इसे और बेहतरीन तरीके से समझ सकते है।
बहुभुज के प्रकार
बहुभुज को मुख्य रूप से 4 प्रकार में बांटा गया है।
- उत्तल बहुभुज
उत्तल बहुभुज एक ऐसा बहुभुज होता है जिसे उसके किसी भी आंतरिक कोण पर एक सीधी रेखा खींचकर पूरी तरह से उसके अंदर ही रखा जा सकता है।
दूसरे शब्दों में कहें तो जिस बहुभुज का कोई भी आंतरिक कोण 180° से अधिक नहीं होता वह उत्तल बहुभुज कहलाता है।
यानी कि अगर आप किसी बहुभुज के अंदर खड़े हो और बिना मुड़े ही सभी भुज को देख सके तो वह उत्तर बहुभुज होगा।
उत्तल बहुभुज के उदाहरण में त्रिभुज, वर्ग, पंचभुज शामिल है।
- नियमित बहुभुज
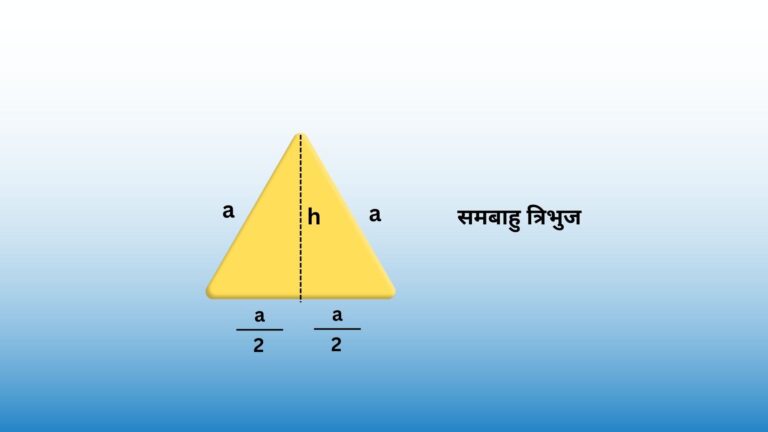
नियमित बहुभुज वह होता है, जिसकी सभी भुजाओं की लंबाई समान होती है और इसके आंतरिक कोण का माप भी समान होता है।
नियमित बहुभुज के उदाहरण में समबाहु त्रिभुज, वर्गाकार इत्यादि शामिल है।
- अनियमित बहुभुज
अनियमित बहुभुज नियमित बहुभुज के विपरीत होता है। यानी कि इसकी सभी भुजा की लंबाई समान नहीं होती और साथ ही आंतरिक कोण के माप भी समान नहीं होते हैं।
अनियमित बहुभुज के उदाहरण में समद्वीबाहू त्रिभुज और विषमबाहु चतुर्भुज शामिल है।
- अवतल बहुभुज
यह एक ऐसा बहुभुज होता है जिसका आंतरिक को 180° से अधिक हो सकता है। यह उत्तल बहुभुज का ठीक उल्टा होता है।
यह एक ऐसा बहुभुज है, जिसे उसके किसी एक आंतरिक कोण पर सीधी रेखा खींचने पर वह रेखा बहुभुज के बाहर से होकर गुजरती है। और ऐसा इसलिए होता है क्योंकि इसका आंतरिक को 180° से अधिक होता है। इसका उपयोग ज्यामिति में बहुत ही काम किया जाता है।
आसान शब्दों में कहे तो इस बहुभुज के अंदर एक या एक से अधिक ऐसे बिंदु होते हैं जहां से आप सभी भुजाओं को नहीं देख सकते हैं।
अवतल बहुभुज के उदाहरण में घोड़े की नाल, तीर का निशान इत्यादि शामिल है।
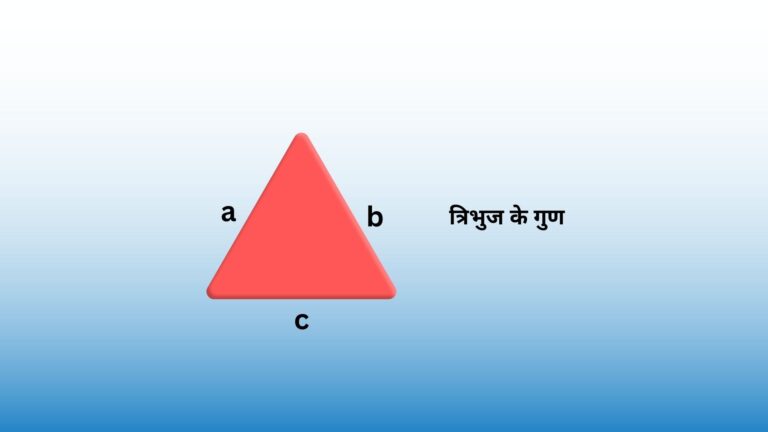
बहुभुज के गुण
बहुभुज के गुण इस प्रकार हैं।
- किसी भी बहुभुज में कम से कम 3 भुजाएँ होनी चाहिए। अधिकतम भुजाओं की कोई सीमा नहीं है।
- किसी n भुजाओं वाले बहुभुज के आंतरिक कोणों का योग (180° * (n – 2)) होता है।
- किसी भी बहुभुज के सभी बाहरी कोणों का योग 360° होता है।
- किसी बहुभुज के दो गैर-संलग्न कोनों को जोड़ने वाली रेखा को बहुभुज का विकर्ण (diagonal) कहते हैं। केवल त्रिभुजों और चतुर्भुजों में विकर्ण हो सकते हैं।
बहुभुज का सूत्र
बहुभुज से संबंधित दो सूत्र हैं, जिसमे बहुभुज का आयतन और बहुभुज का क्षेत्रफल निकाला जाता है।
अलग-अलग बहुभुज के क्षेत्रफल एवं परिमाप निकालने के लिए अलग-अलग सूत्र होते हैं। क्योंकि यह सूत्र इस बात पर निर्भर करता है कि बहुभुज नियमित है या अनियमित।
उदाहरण के लिए, अगर आप त्रिभुज का क्षेत्रफल निकलते हैं तो इसके लिए सूत्र उसके आधार और ऊंचाई के आधे गुणनखंड के बराबर होगा।
लेकिन वही अगर आप किसी बहुभुज के परिमाप को निकालना चाहते हैं तो यहां पर आपको सभी भुज की लंबाई को जोड़ना होगा।
यहां पर हम आपको टेबल के माध्यम से अलग-अलग बहुभूजों की परिमाप एवं क्षेत्रफल निकालने के सूत्र की जानकारी दे रहे हैं।
| बहुभुज का नाम | क्षेत्रफल | परिमाप |
| त्रिभुज (Triangle) | ½ आधार (base) × ऊँचाई (height) | भुजा a + भुजा b + भुजा c |
| वर्ग (Square) | भुजा का वर्ग (side²) | 4 × भुजा (side) |
| आयत (Rectangle) | लंबाई (length) × चौड़ाई (breadth) | 2 (लंबाई + चौड़ाई) |
| समांतर चतुर्भुज (Parallelogram) | आधार (base) × ऊँचाई (height) | 2 (आसन्न भुजाओं का योग) |
| समलम्ब चतुर्भुज (Trapezoid) | क्षेत्रफल = 1/2 (समांतर भुजाओं का योग) × ऊँचाई (height) | सभी भुजाओं का योग |
| समचतुर्भुज (Rhombus) | ½ (विकर्णों का गुणनफल) | 4 × भुजा (side) |
| पंचभुज (Pentagon) | 4√5(5+2√5)s2 | सभी पाँच भुजाओं का योग |
| षट्भुज (Hexagon) | 3√3/2 (भुजा का वर्ग) | सभी छह भुजाओं का योग |
बहुभुज के कोण
तो जैसा कि हमने आपको बताया बहुभुज में जितनी भुजाएं होती हैं, उतने ही शीर्ष होते हैं। साथ ही इसके हर शीर्ष पर एक कोण बनता है।
तो इन बहुभुज में बनने वाले को को दो भागों में विभाजित किया गया है। जिसे हम आंतरिक कोण और बाह्य कोण कहते हैं।
1. बहुभुज का आंतरिक कोण
बहुभुज के किसी भी दो भुजाओं के बीच जो को बनता है, उसे आंतरिक कोण कहते हैं। किसी भी n भुजाओं वाले बहुभुज के आंतरिक कोणों के माप का योग एक निश्चित सूत्र द्वारा निकाला जाता है।
आंतरिक कोणों का योग = 180° * (n – 2)
उदाहरण,
एक चतुर्भुज में चार भुजाएँ होती हैं, इसलिए सभी आंतरिक कोणों का योग इस प्रकार दिया जाता है:
4 भुजाओं वाले बहुभुज के आंतरिक कोणों का योग = (4 – 2) × 180°
= 2 × 180°
= 360°
2. बहुभुज का बाह्य कोण
किसी भी बहुभुज के हर शीर्ष पर आंतरिक कोण और उससे संबंधित बाय कोण एक दूसरे के पूरक होते हैं।
यानी कि बहुभुज का बाह्य कोण ज्ञात करने के लिए निम्न सूत्र का उपयोग किया जाएगा।
किसी भी n भुजाओं वाले बहुभुज के प्रत्येक बाहरी को का माप
बाहरी कोण का माप = 360° / n
विभिन्न प्रकार के बहुभुज के नाम
जैसा कि आप जानते हैं बहुभुज कई प्रकार के होते हैं तो यहां पर हम आपके साथ सभी भुजाओं वाले बहुभुज के नाम शेयर कर रहे हैं।
| भुजाओं की संख्या (Number of Sides) | बहुभुज का नाम (Name of Polygon) | हिंदी नाम (Hindi Name) |
| 3 | त्रिभुज (Triangle) | तिकोण |
| 4 | चतुर्भुज (Quadrilateral) | चौकोर |
| 5 | पंचभुज (Pentagon) | पंचकोण |
| 6 | षट्भुज (Hexagon) | षटकोण |
| 7 | सप्तभुज (Heptagon) | सप्तकोण |
| 8 | अष्टभुज (Octagon) | अष्टकोण |
| 9 | नवभुज (Nonagon) | नवकोण |
| 10 | दशभुज (Decagon) | दशकोण |
| 11 | एकादशभुज (Hendecagon) | एकादशकोण |
| 12 | द्वादशभुज (Dodecagon) | द्वादशकोण |
निष्कर्ष
आज के इस लेख में हमने बहुभुज की परिभाषा से संबंधित विस्तार पूर्वक जानकारी प्राप्त की। उम्मीद है कि इस लेख के माध्यम से आपको बहुभुज से संबंधित अवधारणा समझ आप आई होगी। यदि आप इस विषय पर कोई अन्य जानकारी पाना चाहते हो तो हमें कमेंट करके जरूर बताएं।समझा आप आई होगी। यदि आप इस विषय पर कोई अन्य जानकारी पाना चाहते हो तो हमें कमेंट करके जरूर बताएं।